题目内容
已知函数f(x)=ax+b|x-1|(x∈R),若b>0,且关于x的不等式f(x)<0的解集中整数恰有2个,则
的取值范围为 .
| a |
| b |
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:由于f(x)=ax+b|x-1|=
,依题意,可作出函数的图象,列出相应的不等式组,解之即可.
|
解答:
 解:f(x)=ax+b|x-1|=
解:f(x)=ax+b|x-1|=
,
∵b>0,
∴f(0)=b>0,
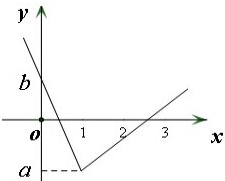
且关于x的不等式f(x)<0的解集中整数恰有2个,作图如下:
则需
,即
,
解得:-
≤
<-
.
故答案为:[-
,-
).
 解:f(x)=ax+b|x-1|=
解:f(x)=ax+b|x-1|=
|
∵b>0,
∴f(0)=b>0,
且关于x的不等式f(x)<0的解集中整数恰有2个,作图如下:
则需
|
|
解得:-
| 2 |
| 3 |
| a |
| b |
| 1 |
| 2 |
故答案为:[-
| 2 |
| 3 |
| 1 |
| 2 |
点评:本题考查函数的最值及其几何意义,考查数形结合的数学思想,考查学生分析解决问题的能力,属于中档题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
复数z=
的虚部为( )
| 5+i |
| 1+i |
| A、2 | B、-2 | C、2i | D、-2i |