题目内容
5.已知抛物线x2=2py(p>0),过其焦点$F(0,\frac{p}{2})$的直线l与抛物线相交于A,B两点,设A,B两点的坐标分别为A(x1,y1),B(x2,y2).求证:(1)x1•x2=-p2
(2)y1•y2=$\frac{p^2}{4}$.
分析 (1)设过其焦点$F(0,\frac{p}{2})$的直线l的方程为y=kx+$\frac{p}{2}$,代入抛物线x2=2py,运用韦达定理,即可得证;
(2)由A,B在抛物线x2=2py上,代入方程,两式相乘即可得证.
解答 证明:(1)设过其焦点$F(0,\frac{p}{2})$的直线l的方程为y=kx+$\frac{p}{2}$,
代入抛物线x2=2py,可得
x2-2pkx-p2=0,
由A(x1,y1),B(x2,y2),可得
x1x2=-p2;
(2)由A,B在抛物线x2=2py上,可得
y1=$\frac{{{x}_{1}}^{2}}{2p}$,y2=$\frac{{{x}_{2}}^{2}}{2p}$,
即有y1y2=$\frac{({x}_{1}{x}_{2})^{2}}{4{p}^{2}}$=$\frac{{p}^{4}}{4{p}^{2}}$=$\frac{{p}^{2}}{4}$.
点评 本题考查抛物线的方程的运用,注意联立直线方程和抛物线方程,消去一个变量,运用韦达定理,考查运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
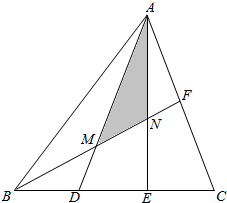 △ABC中,D、E三等分BC,F为AC的中点,BF分别与AD、AE交于M、N.试求△AMN与△ABC面积之比.
△ABC中,D、E三等分BC,F为AC的中点,BF分别与AD、AE交于M、N.试求△AMN与△ABC面积之比.