题目内容

10．函数y=|tanx|的对称轴是x=$\frac{π}{2}k$，k∈Z．

分析 根据正切函数的图象及性质，y=|tanx|的图象是y=tanx把x轴的下部分翻折到x轴的上方可得到的直接得答案．

解答 解：函数y=|tanx|的图象是y=tanx把x轴的下部分翻折到x轴的上方可得到的．
∴函数y=|tanx|的对称轴是x=$\frac{π}{2}k$，k∈Z．
故答案为：x=$\frac{π}{2}k$，k∈Z．

点评 本题考查了y=|tanx|的图象与y=tanx图象的关系，属于基础题．

练习册系列答案
相关题目
20．已知函数f（x）=lg（x2+ax+b）的定义域为A，$g（x）=\sqrt{k{x^2}+4x+k+3}$的定义域为B．
（1）若B=R，求k的取值范围；
（2）若（∁RA）∩B=B，（∁RA）∪B={x|-2≤x≤3}，求实数a，b的值及实数k的取值范围．
1．要得到y=sinx的图象只需将$y=sin（\frac{x}{2}+\frac{π}{3}）$的图象（　　）
A．先向左平移$\frac{2π}{3}$单位，再将图象上各点的横坐标缩短至原来的$\frac{1}{2}$
B．先向右平移$\frac{2π}{3}$单位，再将图象上各点的横坐标缩短至原来的$\frac{1}{2}$
C．先将图象上各点的横坐标缩短至原来的$\frac{1}{2}$，再将图象向左平移$\frac{π}{3}$单位
D．先将图象上各点横坐标扩大为原来的2倍，再将图象向右平移$\frac{π}{3}$单位
18．若无穷数列{an}满足：?k∈N*，对于$?n≥{n_0}（{n_0}∈{N^*}）$，都有an+k-an=d（其中d为常数），则称{an}具有性质“P（k，n0，d）”．
（Ⅰ）若{an}具有性质“P（3，2，0）”，且a2=3，a4=5，a6+a7+a8=18，求a3；
（Ⅱ）若无穷数列{bn}是等差数列，无穷数列{cn}是公比为正数的等比数列，b1=c3=2，b3=c1=8，an=bn+cn，判断{an}是否具有性质“P（2，1，0）”，并说明理由；
（Ⅲ）设{an}既具有性质“P（i，2，d1）”，又具有性质“P（j，2，d2）”，其中i，j∈N*，i＜j，i，j互质，求证：{an}具有性质“$P（j-i，i+2，\frac{j-i}{i}{d_1}）$”．
5．某几何体的三视图如图所示，则该几何体的外接球的体积为（　　）
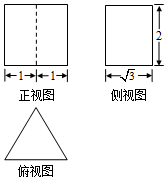
A．$\frac{4}{3}π$B．$\frac{{32\sqrt{3}}}{27}π$C．$\frac{{28\sqrt{3}}}{27}π$D．$\frac{{28\sqrt{21}}}{27}π$
15．现有三张卡片，正面分别标有数字1，2，3，背面完全相同，将卡片洗匀，背面向上放置，甲、乙二人轮流抽取卡片，每人每次抽一张，抽取后不放回，甲先抽．若二人约定，先抽到标有偶数的卡片者获胜，则甲获胜的概率是（　　）
A．$\frac{1}{3}$B．$\frac{1}{2}$C．$\frac{2}{3}$D．$\frac{5}{6}$
2．从一批含有11只正品，2只次品的产品中，不放回地抽取3次，每次抽取1只，设抽得次品数为X，则E（5X+1）的值为（　　）
A．$\frac{42}{13}$B．$\frac{12}{13}$C．$\frac{41}{11}$D．$\frac{6}{13}$
19．在△ABC中，角A，B，C的对边分别为a，b，c，且A=30°，B=15°，a=3，则c的值为（　　）
A．6B．$\frac{3}{2}$C．3$\sqrt{3}$D．3$\sqrt{2}$
20．已知函数$y=acos（2x+\frac{π}{3}）+3$，$x∈[0，\frac{π}{2}]$的最大值为4，则正实数a的值为2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网