题目内容
13.已知函数f(x)=2cosx-3sinx的导数为f'(x),则f'(x)=( )| A. | f'(x)=-2sinx-3cosx | B. | f'(x)=-2cosx+3sinx | ||
| C. | f'(x)=-2sinx+3cosx | D. | f'(x)=2sinx-3cosx |
分析 根据基本导数公式求导即可
解答 解:f'(x)=-2sinx-3cosx,
故选:A
点评 本题考查导数的运算法则,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.要得到y=sinx的图象只需将$y=sin(\frac{x}{2}+\frac{π}{3})$的图象( )
| A. | 先向左平移$\frac{2π}{3}$单位,再将图象上各点的横坐标缩短至原来的$\frac{1}{2}$ | |
| B. | 先向右平移$\frac{2π}{3}$单位,再将图象上各点的横坐标缩短至原来的$\frac{1}{2}$ | |
| C. | 先将图象上各点的横坐标缩短至原来的$\frac{1}{2}$,再将图象向左平移$\frac{π}{3}$单位 | |
| D. | 先将图象上各点横坐标扩大为原来的2倍,再将图象向右平移$\frac{π}{3}$单位 |
5.某几何体的三视图如图所示,则该几何体的外接球的体积为( )
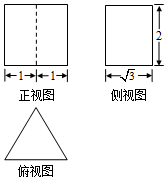

| A. | $\frac{4}{3}π$ | B. | $\frac{{32\sqrt{3}}}{27}π$ | C. | $\frac{{28\sqrt{3}}}{27}π$ | D. | $\frac{{28\sqrt{21}}}{27}π$ |
2.从一批含有11只正品,2只次品的产品中,不放回地抽取3次,每次抽取1只,设抽得次品数为X,则E(5X+1)的值为( )
| A. | $\frac{42}{13}$ | B. | $\frac{12}{13}$ | C. | $\frac{41}{11}$ | D. | $\frac{6}{13}$ |