题目内容
15.先把函数$y=2sin({2x+\frac{π}{6}})$的图象上的所有点向左平移$\frac{π}{6}$个单位长度,再把所有点的横坐标伸长到原来的$\frac{1}{2}$倍,纵坐标不变,得到的图象对应的函数解析式是y=2cos4x.分析 利用函数y=Asin(ωx+φ)的图象变换规律,诱导公式,得出结论.
解答 解:把函数$y=2sin({2x+\frac{π}{6}})$的图象上的所有点向左平移$\frac{π}{6}$个单位长度,可得y=2sin(2x+$\frac{π}{3}$+$\frac{π}{6}$)=2cos2x的图象;
再把所有点的横坐标伸长到原来的$\frac{1}{2}$倍,纵坐标不变,得到的图象对应的函数为y=2cos4x,
故答案为:y=2cos4x.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,诱导公式,属于基础题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
14.已知直线l过点P(1,2),且与x轴、y轴的正半轴分别交于A,B两点,则当△AOB的面积取得最小值时,直线l的方程为( )
| A. | 2x+y-4=0 | B. | x-2y+3=0 | C. | x+y-3=0 | D. | x-y+1=0 |
10.不等式lnx+x-1<0的解集为( )
| A. | $(0,\frac{e}{4})$ | B. | $(0,\frac{e}{2})$ | C. | (0,1) | D. | (1,+∞) |
5.某几何体的三视图如图所示,则该几何体的外接球的体积为( )
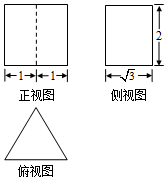

| A. | $\frac{4}{3}π$ | B. | $\frac{{32\sqrt{3}}}{27}π$ | C. | $\frac{{28\sqrt{3}}}{27}π$ | D. | $\frac{{28\sqrt{21}}}{27}π$ |