题目内容
17.(1)已知a,b∈R,i是虚数单位,若(a+i)(1+i)=bi,求a,b;(2)设m∈R,m2+m-2+(m2-1)i是纯虚数,其中i是虚数单位,求m.
分析 (1)利用复数代数形式的乘法运算展开等式左边,再由复数相等的条件列式求得a,b的值;
(2)直接利用实部为0且虚部不为0求得m值.
解答 解:(1)由(a+i)(1+i)=bi,得a-1+(a+1)i=bi,
由复数相等,知:a-1=0 a+1=b,
解得:a=1,b=2;
(2)∵m2+m-2+(m2-1)i是纯虚数,
∴$\left\{\begin{array}{l}{{m}^{2}+m-2=0}\\{{m}^{2}-1≠0}\end{array}\right.$,解答m=-2.
点评 本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.某几何体的三视图如图所示,则该几何体的外接球的体积为( )
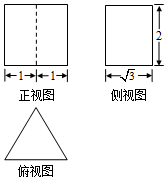

| A. | $\frac{4}{3}π$ | B. | $\frac{{32\sqrt{3}}}{27}π$ | C. | $\frac{{28\sqrt{3}}}{27}π$ | D. | $\frac{{28\sqrt{21}}}{27}π$ |
2.从一批含有11只正品,2只次品的产品中,不放回地抽取3次,每次抽取1只,设抽得次品数为X,则E(5X+1)的值为( )
| A. | $\frac{42}{13}$ | B. | $\frac{12}{13}$ | C. | $\frac{41}{11}$ | D. | $\frac{6}{13}$ |
6.设等比数列{an}的前n项和为Sn,若$\frac{{S}_{6}}{{S}_{3}}$=7,则$\frac{{S}_{9}}{{S}_{6}}$=( )
| A. | 2 | B. | $\frac{7}{3}$ | C. | $\frac{13}{4}$ | D. | $\frac{43}{7}$ |
7.抛物线的顶点在原点,焦点是椭圆4x2+y2=1的一个焦点,则此抛物线的焦点到准线的距离是( )
| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{1}{2}\sqrt{3}$ | D. | $\frac{1}{4}\sqrt{3}$ |