题目内容
14.下列结论不正确的是( )①.$\frac{1}{{{2^{10}}}}+\frac{1}{{{2^{10}}+1}}+\frac{1}{{{2^{10}}+2}}+…+\frac{1}{{{2^{11}}-1}}>1$
②若|a|<1,则|a+b|-|a-b|>2
③lg9•lg11<1
④若x>0,y>0,则$\frac{x+y}{1+x+y}<\frac{x}{1+x}+\frac{y}{1+y}$.
| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①③ |
分析 由不等式的左边由210项,且小于$\frac{1}{{2}^{10}}$,即可判断①;运用绝对值不等式的性质,即可判断②;
运用基本不等式,即可判断③;运用不等式的放缩法,即可判断④.
解答 解:对于①,$\frac{1}{{2}^{10}}$+$\frac{1}{{2}^{10}+1}$+$\frac{1}{{2}^{10}+2}$+…+$\frac{1}{{2}^{11}-1}$<$\frac{1}{{2}^{10}}$+$\frac{1}{{2}^{10}}$+…+$\frac{1}{{2}^{10}}$=1,故①不正确;
对于②若|a|<1,则|a+b|-|a-b|≤|(b+a)-(b-a)|=2|a|<2,故②不正确;
对于③,lg9•lg11<($\frac{lg9+lg11}{2}$)2<$\frac{l{g}^{2}100}{4}$=1,故③正确;
对于④,若x>0,y>0,由$\frac{x}{1+x}$>$\frac{x}{1+x+y}$,$\frac{y}{1+y}$>$\frac{y}{1+x+y}$,
可得$\frac{x+y}{1+x+y}<\frac{x}{1+x}+\frac{y}{1+y}$,故④正确.
故选:A.
点评 本题考查命题的真假判断和运用,主要是不等式的放缩和基本不等式的运用,以及不等式的性质,考查推理能力和判断能力,属于中档题.

练习册系列答案
相关题目
5.某几何体的三视图如图所示,则该几何体的外接球的体积为( )
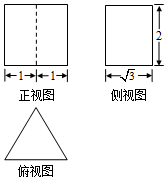

| A. | $\frac{4}{3}π$ | B. | $\frac{{32\sqrt{3}}}{27}π$ | C. | $\frac{{28\sqrt{3}}}{27}π$ | D. | $\frac{{28\sqrt{21}}}{27}π$ |
2.从一批含有11只正品,2只次品的产品中,不放回地抽取3次,每次抽取1只,设抽得次品数为X,则E(5X+1)的值为( )
| A. | $\frac{42}{13}$ | B. | $\frac{12}{13}$ | C. | $\frac{41}{11}$ | D. | $\frac{6}{13}$ |
19.在△ABC中,角A,B,C的对边分别为a,b,c,且A=30°,B=15°,a=3,则c的值为( )
| A. | 6 | B. | $\frac{3}{2}$ | C. | 3$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
6.设等比数列{an}的前n项和为Sn,若$\frac{{S}_{6}}{{S}_{3}}$=7,则$\frac{{S}_{9}}{{S}_{6}}$=( )
| A. | 2 | B. | $\frac{7}{3}$ | C. | $\frac{13}{4}$ | D. | $\frac{43}{7}$ |