题目内容
1.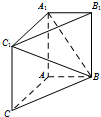 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.(Ⅰ)求证:AA1⊥平面ABC;
(Ⅱ)求二面角A1-BC1-B1的余弦值.
分析 (I)推导出AA1⊥AC,由平面ABC⊥平面AA1C1C,能证明AA1⊥平面ABC.
(II)取A为坐标原点,分别以$\overrightarrow{AC}$,$\overrightarrow{AB}$,$\overrightarrow{AA1}$为x,y,z轴方向,建立空间直角坐标系,利用向量法能求出二面角A1-BC1-B1的余弦值.
解答 证明:(I)∵AA1C1C是正方形,∴AA1⊥AC.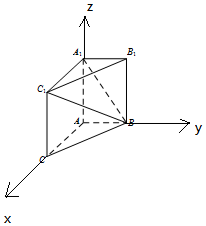
又∵平面ABC⊥平面AA1C1C,
平面ABC∩平面AA1C1C=AC,
∴AA1⊥平面ABC.
解:(II)由AC=4,BC=5,AB=3.∴AC2+AB2=BC2,∴AB⊥AC.
取A为坐标原点,分别以$\overrightarrow{AC}$,$\overrightarrow{AB}$,$\overrightarrow{AA1}$为x,y,z轴方向,建立空间直角坐标系,
则A1(0,0,4),B(0,3,0),B1(0,3,4),C1(4,0,4),
∴$\overrightarrow{B{C}_{1}}$=(4,-3,4),$\overrightarrow{B{A}_{1}}$=(0,-3,4),$\overrightarrow{B{B}_{1}}$=(0,0,4).
设平面A1BC1的法向量为$\overrightarrow{n}$=(x,y,z),平面B1BC1的法向量为$\overrightarrow{m}$=(a,b,c).
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{B{C}_{1}}=4x-3y+4z=0}\\{\overrightarrow{n}•\overrightarrow{B{A}_{1}}=-3y+4z=0}\end{array}\right.$,令y=4,得$\overrightarrow{n}$=(0,4,3).
$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{B{C}_{1}}=4a-3b+4c=0}\\{\overrightarrow{m}•\overrightarrow{B{B}_{1}}=4c=0}\end{array}\right.$,令c=3,得$\overrightarrow{m}$=(3,4,0).
cos<$\overrightarrow{n},\overrightarrow{m}$>=$\frac{\overrightarrow{n}•\overrightarrow{m}}{|\overrightarrow{n}|•|\overrightarrow{m}|}$=$\frac{16}{\sqrt{25}•\sqrt{25}}$=$\frac{16}{25}$,
∴二面角A1-BC1-B1的余弦值为$\frac{16}{25}$.
点评 本题考查线面垂直、面面垂直的判定、性质得灵活应用,考查二面角概念及其求法,化归与转化的思想的应用,考查逻辑推理、运算、空间想象能力.属中档题.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案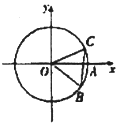 ∠AOB如图,⊙O与x轴的正半轴交点为A,点B,C在⊙O上,且$B(\frac{3}{5},-\frac{4}{5})$,点C在第一象限,∠AOC=α,BC=1,则$cos(\frac{5π}{6}-α)$=( )
∠AOB如图,⊙O与x轴的正半轴交点为A,点B,C在⊙O上,且$B(\frac{3}{5},-\frac{4}{5})$,点C在第一象限,∠AOC=α,BC=1,则$cos(\frac{5π}{6}-α)$=( )| A. | $-\frac{4}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
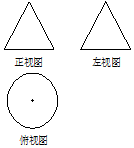 如图,一个空间几何体正视图与左视图为全等的等边三角形,俯视图为一个半径为1的圆及其圆心,那么这个几何体的表面积为( )
如图,一个空间几何体正视图与左视图为全等的等边三角形,俯视图为一个半径为1的圆及其圆心,那么这个几何体的表面积为( )| A. | π | B. | 3π | C. | 2π | D. | $π+\sqrt{3}$ |
| A. | $-\frac{1}{7}$ | B. | $\frac{1}{7}$ | C. | -7 | D. | 7 |
| A. | (¬p)∧q | B. | p∧q | C. | p∨(¬q) | D. | (¬p)∧(¬q) |
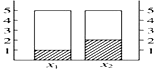
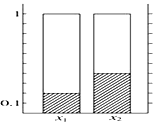
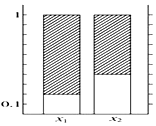
 根据下面列联表作出的条形图中正确的有( )
根据下面列联表作出的条形图中正确的有( )
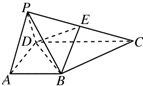 已知在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,2AB=2AD=CD,侧面PAD是正三角形且垂直于底面ABCD,E是PC的中点.
已知在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,2AB=2AD=CD,侧面PAD是正三角形且垂直于底面ABCD,E是PC的中点.