题目内容
7.在直角坐标系xOy中,曲线C:$\left\{\begin{array}{l}{x=\sqrt{2}cosa+1}\\{y=\sqrt{2}sina+1}\end{array}\right.$(α为参数),在以O为极点,x轴的非负半轴为极轴的极坐标系中,直线l的极坐标方程为:ρsin(θ+$\frac{π}{4}$)=m(m∈R).(Ⅰ)求直线l的直角坐标方程;
(Ⅱ)若曲线C上存在点P到直线l的距离为$\frac{\sqrt{2}}{2}$,求实数m的取值范围.
分析 (Ⅰ)直线l的极坐标方程展开得:$ρsinθ+ρcosθ-\sqrt{2}m$=0,由此能求出直线l的直角坐标方程.
(Ⅱ)曲线C的普通方程为:(x-1)2+(y-1)2=2,曲线C是一个圆,圆心C到直线l的距离$d=\frac{|1+1-\sqrt{2}m|}{\sqrt{2}}$$≤\frac{3\sqrt{2}}{2}$,由此能求出结果.
解答 解:(Ⅰ)直线l的极坐标方程为:ρsin(θ+$\frac{π}{4}$)=m(m∈R).
展开得:$ρsinθ+ρcosθ-\sqrt{2}m$=0,…(3分)
所以直线l的直角坐标方程为:x+y-$\sqrt{2}m$=0.…(5分)
(Ⅱ)曲线C的普通方程为:(x-1)2+(y-1)2=2,
所以曲线C是一个圆;…(7分)
由已知可得,圆心C到直线l的距离$d=\frac{|1+1-\sqrt{2}m|}{\sqrt{2}}$$≤\frac{3\sqrt{2}}{2}$,…(9分)
解得-$\frac{\sqrt{2}}{2}≤m≤\frac{5\sqrt{2}}{2}$.…(10分)
点评 本题考查直线的直角坐标方程的求法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意极坐标方程、直角坐标方程互化公式的合理运用.

练习册系列答案
相关题目
17.函数$f(x)=\frac{{3{x^2}}}{{\sqrt{1-x}}}+lg(-3{x^2}+5x+2)$的定义域是( )
| A. | (-$\frac{1}{3}$,+∞) | B. | (-$\frac{1}{3}$,1) | C. | (-$\frac{1}{3}$,$\frac{1}{3}$) | D. | (-∞,-$\frac{1}{3}$) |
15.下列函数中,既是偶函数,又在区间(0,3)内是减函数的是( )
| A. | y=2x-2-x | B. | y=cosx | C. | y=log2|x| | D. | y=x+x-1 |
2.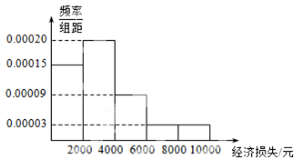 适逢暑假,小王在某小区调查了50户居民由于洪灾造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图(如图).
适逢暑假,小王在某小区调查了50户居民由于洪灾造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图(如图).
(Ⅰ)小王向班级同学发出为该小区居民捐款的倡议.若先从损失超过6000元的居民中随机抽出2户进行捐款援助,求这2户不在同一分组的概率;
(Ⅱ)洪灾过后小区居委会号召小区居民为洪灾重灾区捐款,小王调查的50户居民的捐款情况如表,在表格空白处填写正确的数字,并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d为样本容量).
 适逢暑假,小王在某小区调查了50户居民由于洪灾造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图(如图).
适逢暑假,小王在某小区调查了50户居民由于洪灾造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图(如图).(Ⅰ)小王向班级同学发出为该小区居民捐款的倡议.若先从损失超过6000元的居民中随机抽出2户进行捐款援助,求这2户不在同一分组的概率;
(Ⅱ)洪灾过后小区居委会号召小区居民为洪灾重灾区捐款,小王调查的50户居民的捐款情况如表,在表格空白处填写正确的数字,并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
| 经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
| 捐款超过500元 | 30 | 9 | 39 |
| 捐款不超过500元 | 5 | 6 | 11 |
| 合计 | 35 | 15 | 50 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
12.设函数$f(x)=\left\{\begin{array}{l}{log_{\frac{1}{2}}}(x+1),0≤x≤1\\ f(x-1),x>1\end{array}\right.$,则$f(\sqrt{2})$的值是( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
16.某空间几何体的三视图如图所示,则此几何体的体积为( )


| A. | $\frac{5π}{3}$ | B. | $\frac{10π}{3}$ | C. | $\frac{11π}{3}$ | D. | $\frac{22π}{3}$ |
 如图所示的三角形数阵角“莱布尼兹调和三角形”,它是由整数的倒数组成的,第n行有n个数,且两端的数均为$\frac{1}{n}({n≥2})$,每个数使它下一行左右相邻两个数的和,如$\frac{1}{1}=\frac{1}{2}+\frac{1}{2},\frac{1}{2}=\frac{1}{3}+\frac{1}{6},\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$,则第7行第5个数(从左到右)为$\frac{1}{105}$.
如图所示的三角形数阵角“莱布尼兹调和三角形”,它是由整数的倒数组成的,第n行有n个数,且两端的数均为$\frac{1}{n}({n≥2})$,每个数使它下一行左右相邻两个数的和,如$\frac{1}{1}=\frac{1}{2}+\frac{1}{2},\frac{1}{2}=\frac{1}{3}+\frac{1}{6},\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$,则第7行第5个数(从左到右)为$\frac{1}{105}$.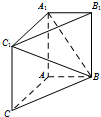 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.