题目内容
函数y=
sin2x+4sin2x,x∈R的值域是 .
| 1 |
| 2 |
考点:三角函数的最值
专题:三角函数的求值
分析:化简可得y=
sin(2x-θ)+2,其中tanθ=4,由sin(2x-θ)的值域为[-1,1]和不等式的性质可得.
| ||
| 2 |
解答:
解:化简可得y=
sin2x+4sin2x
=
sin2x+4•
=
sin2x-2cos2x+2
=
sin(2x-θ)+2,其中tanθ=4,
∵sin(2x-θ)的值域为[-1,1],
∴y=
sin(2x-θ)+2的值域为[2-
,2+
]
故答案为:[2-
,2+
]
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1-cos2x |
| 2 |
=
| 1 |
| 2 |
=
| ||
| 2 |
∵sin(2x-θ)的值域为[-1,1],
∴y=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
故答案为:[2-
| ||
| 2 |
| ||
| 2 |
点评:本题考查三角函数的最值,属基础题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的侧面积是( )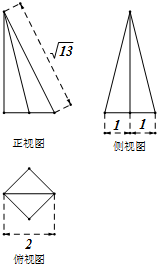

| A、2 | ||||
B、3
| ||||
C、3
| ||||
D、3
|
双曲线
-
=1的焦点到渐近线的距离为( )
| x2 |
| 4 |
| y2 |
| 12 |
A、2
| ||
| B、2 | ||
C、
| ||
| D、1 |
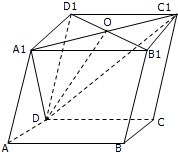 如图所示,在平行六面体ABCD-A1B1C1D1中,O是B1D1的中点,求证:
如图所示,在平行六面体ABCD-A1B1C1D1中,O是B1D1的中点,求证: