题目内容
已知二次函数f(x)的二次项系数为a,且不等式f(x)>-2x的解集为(1,3).
(1)若当x≤-1时,不等式f(x)+5a<0恒成立,求a的取值范围;
(2)当x∈[0,2]时,f(x)的值域是[-6,-
],求实数a.
(1)若当x≤-1时,不等式f(x)+5a<0恒成立,求a的取值范围;
(2)当x∈[0,2]时,f(x)的值域是[-6,-
| 3 |
| 2 |
考点:函数恒成立问题,二次函数在闭区间上的最值,一元二次不等式的解法
专题:函数的性质及应用,不等式的解法及应用
分析:(1)由f(x)>-2x的解集为(1,3),得f(x)+2x=a(x-1)(x-3),从而求得函数f(x)的解析式,代入f(x)+5a<0,利用“三个二次”的结合列不等式组求解a的取值范围;
(2)求出二次函数f(x)的对称轴,对对称轴分类求解当x∈[0,2]时,f(x)的值域是[-6,-
]的实数a的值.
(2)求出二次函数f(x)的对称轴,对对称轴分类求解当x∈[0,2]时,f(x)的值域是[-6,-
| 3 |
| 2 |
解答:
解:(1)∵f(x)>-2x的解集为(1,3).
∴f(x)+2x=a(x-1)(x-3),
∴a<0,
f(x)=a(x-1)(x-3)-2x=ax2-(2+4a)x+3a,
∴不等式f(x)+5a<0即为ax2-(2+4a)x+8a<0,
要使ax2-(2+4a)x+8a<0在x≤-1时恒成立,
则
①或
②,
解①得:a<-
,解②得:a<-
.
∴当x≤-1时,不等式f(x)+5a<0恒成立的实数a的取值范围是(-∞,-
);
(2)f(x)=ax2-(2+4a)x+3a,
当a<0时,对称轴为x=2+
<2,
若2+
≤0,即-
≤a<0,则
,a不存在;
若0<2+
≤1,即-1≤a<-
,则
,a不存在;
若1<2+
<2,即a<-1,则
,解得a=-2.
综上,实数a的值为-2.
∴f(x)+2x=a(x-1)(x-3),
∴a<0,
f(x)=a(x-1)(x-3)-2x=ax2-(2+4a)x+3a,
∴不等式f(x)+5a<0即为ax2-(2+4a)x+8a<0,
要使ax2-(2+4a)x+8a<0在x≤-1时恒成立,
则
|
|
解①得:a<-
| 1 |
| 3 |
| 1 |
| 5 |
∴当x≤-1时,不等式f(x)+5a<0恒成立的实数a的取值范围是(-∞,-
| 1 |
| 5 |
(2)f(x)=ax2-(2+4a)x+3a,
当a<0时,对称轴为x=2+
| 1 |
| a |
若2+
| 1 |
| a |
| 1 |
| 2 |
|
若0<2+
| 1 |
| a |
| 1 |
| 2 |
|
若1<2+
| 1 |
| a |
|
综上,实数a的值为-2.
点评:本题考查了函数解析式的求解及常用方法,考查了二次函数最值的求法,体现了数学转化思想方法和分类讨论的数学思想方法,是中高档题.

练习册系列答案
相关题目
已知函数y=5sinωx(ω>0)的图象与直线y-5=0相邻的两个公共点之间的距离为
,则ω的值为( )
| π |
| 2 |
A、
| ||
| B、2 | ||
C、
| ||
| D、4 |
25人排成5×5方阵,从中选出3人分别担任队长、副队长、纪律监督员,要求这3人任两人都不同行也不同列,则不同的任职方法数为( )
| A、7200种 |
| B、1800种 |
| C、3600种 |
| D、4500种 |
已知抛物线y=ax2-2x+1与x轴没有交点,那么该抛物线的顶点所在的象限是( )
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |
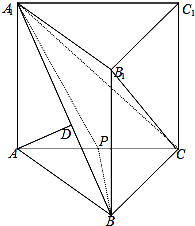 如图,直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.P为AC的中点.
如图,直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.P为AC的中点.