题目内容
 在平面直角坐标系xOy中,已知圆C经过A(2,-2),B(1,1)两点,且圆心在直线x-2y-2=0上.
在平面直角坐标系xOy中,已知圆C经过A(2,-2),B(1,1)两点,且圆心在直线x-2y-2=0上.(1)求圆C的标准方程;
(2)设直线l与圆C相交于P,Q两点,坐标原点O到直线l的距离为
| 1 |
| 5 |
| 2 |
| 5 |
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(1)求出线段AB的垂直平分线的方程,与直线x-2y-2=0联立,求得圆心坐标,再求出圆的半径,即可求圆C的标准方程;
(2)求出PQ=4,分类讨论,利用坐标原点O到直线l的距离为
,即可求直线l的方程.
(2)求出PQ=4,分类讨论,利用坐标原点O到直线l的距离为
| 1 |
| 5 |
解答:
解:(1)因为A(2,-2),B(1,1),所以kAB=-3,AB的中点为(
,-
),
故线段AB的垂直平分线的方程为y+
=
(x-
),即x-3y-3=0,
由
,解得圆心坐标为(0,-1).…(4分)
所以半径r满足r2=12+(-1-1)2=5.…(6分)
故圆C的标准方程为x2+(y+1)2=5.…(7分)
(2)因为S△OPQ=
×PQ×
=
,所以PQ=4.
①当直线l与x轴垂直时,由坐标原点O到直线l的距离为
知,直线l的方程为x=
或x=-
,经验证,此时PQ≠4,不适合题意; …(9分)
②当直线l与x轴不垂直时,设直线l的方程为y=kx+b,
由坐标原点到直线l的距离为d1=
=
,得k2+1=25b2(*),…(11分)
又圆心到直线l的距离为d2=
,所以PQ=2
=2
=4,
即(1+b)2=k2+1(**),…(13分)
由(*),(**)解得
.
综上所述,直线l的方程为3x+4y-1=0或3x-4y+1=0.…(14分)
| 3 |
| 2 |
| 1 |
| 2 |
故线段AB的垂直平分线的方程为y+
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 2 |
由
|
所以半径r满足r2=12+(-1-1)2=5.…(6分)
故圆C的标准方程为x2+(y+1)2=5.…(7分)
(2)因为S△OPQ=
| 1 |
| 2 |
| 1 |
| 5 |
| 2 |
| 5 |
①当直线l与x轴垂直时,由坐标原点O到直线l的距离为
| 1 |
| 5 |
| 1 |
| 5 |
或x=-
| 1 |
| 5 |
②当直线l与x轴不垂直时,设直线l的方程为y=kx+b,
由坐标原点到直线l的距离为d1=
| |b| | ||
|
| 1 |
| 5 |
又圆心到直线l的距离为d2=
| |1+b| | ||
|
| 5-d22 |
5-
|
即(1+b)2=k2+1(**),…(13分)
由(*),(**)解得
|
综上所述,直线l的方程为3x+4y-1=0或3x-4y+1=0.…(14分)
点评:本题考查直线和圆的方程的应用,考查点到直线的距离公式,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
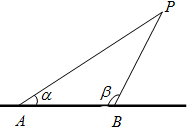 根据国际公法,外国船只不得进入离我国海岸线12海里以内的区域(此为我国领海,含分界线).若外国船只进入我国领海,我方将向其发出警告令其退出.如图,已知直线AB为海岸线,A,B是相距12海里的两个观测站,现发现一外国船只航行于点P处,此时我方测得∠BAP=α,∠ABP=β(0<α<π,0<β<π).
根据国际公法,外国船只不得进入离我国海岸线12海里以内的区域(此为我国领海,含分界线).若外国船只进入我国领海,我方将向其发出警告令其退出.如图,已知直线AB为海岸线,A,B是相距12海里的两个观测站,现发现一外国船只航行于点P处,此时我方测得∠BAP=α,∠ABP=β(0<α<π,0<β<π).