题目内容

求函数y=
1+x
+
2-2x
的最大值．
考点：二维形式的柯西不等式
专题：
分析：由柯西不等式可得y2=（
1+x
+
2-2x
）2≤[12+（
2
）2]（1+x+1-x）=6，即可求出函数的最大值．
解答： 解：由柯西不等式可得y2=（
1+x
+
2-2x
）2≤[12+（
2
）2]（1+x+1-x）=6，
当且仅当
1
1+x
=
2
1-x
，即x=-
1
3
时取等号，
∵y≥0，
∴x=-
1
3
时，y的最大值为
6
．
点评：本题考查二元柯西不等式及应用，考查基本的运算能力，是一道基础题．
练习册系列答案
相关题目
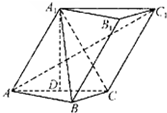已知三棱柱ABC-A1B1C1中，∠BCA=90°，AA1=AC=BC=2，A1在底面ABC上的射影恰为AC的中点D．
（Ⅰ）求证：AC1⊥BA1；
（Ⅱ）求四棱锥A1-BCC1B1的体积．
已知数列{an}的前n项和Sn=n3-10n2（?n∈N*）．
（1）求an；
（2）求集合{n|an＜0，n∈N*}（用列举法表示）．
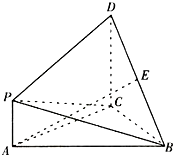如图，△ABC是等边三角形，PA⊥平面ABC，DC∥PA，且DC=AC=2PA=2，E是BD的中点．
（Ⅰ）求证：AE⊥BC；
（Ⅱ）求点D到平面PBC的距离．
已知中心在原点O，焦点在x轴上的椭圆C方程为
x2
a2
+
y2
b2
=1，椭圆上的点到焦点距离最大值为3，离心率e=
1
2
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）A，B为椭圆上的点，△AOB面积为
3
，求证：|OA|2+|OB|2为定值．
设函数f（x）=x3-6x+5，x∈R
（1）求f（x）的单调区间和极值；
（2）若直线y=a与y=f（x）的图象有三个不同的交点，求实数a的取值范围；
（3）已知当x∈（1，+∞）时，f（x）≥k（x-1）恒成立，求实数k的取值范围．
甲乙两个班级均为40人，进行一门考试后，按学生考试成绩及格与不及格进行统计，甲班及格人数为36人，乙班及格人数为24人．
（Ⅰ）根据以上数据建立一个2×2的列联表；
（Ⅱ）试判断能否有99.5%的把握认为“考试成绩与班级有关”？参考公式：K2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)
；n=a+b+c+d
P（K2＞k） 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
设圆（x+1）2+y2=16的圆心为C，A（1，0）是圆内一点，Q为圆周上任意一点，线段AQ的垂直平分线与CQ的连线交于点M．
（1）求点M的轨迹T的方程；
（2）设直线l：y=kx+1-2k恒过点P，且与曲线T相交于不同的两点B、D，若
PB
•
PD
＞
5
4
，试求k的取值范围．
设函数f（x）=2cos（2x-
2π
3
），则下列结论正确的是
 
（写出所有正确的编号）．
①f（x）的最小正周期为π；
②f（x）在区间[
5π
6
，
7π
6
]上单调递增；
③f（x）取得最大值的x的集合为{x|x=
π
3
+
k
2
π，k∈Z}；
④将f（x）的图象向左平移
7π
12
个单位，得到一个奇函数的图象；
⑤当x∈[
π
6
，
5π
12
]时，关于x的方程f（x）-m=0有且只有一个实数根，则m∈[1，
3
）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网