题目内容
已知（1-2x）n（n∈N*）的展开式的偶数项的二项式系数和为32．
（Ⅰ）求n的值；
（Ⅱ）设（1-2x）n=a0+a1x+a2x2+…+anxn（n∈N*），求a1+a2+a3+…+an的值．
（Ⅰ）求n的值；
（Ⅱ）设（1-2x）n=a0+a1x+a2x2+…+anxn（n∈N*），求a1+a2+a3+…+an的值．
考点：二项式系数的性质,二项式定理的应用
专题：二项式定理
分析：（Ⅰ）由题意可得 2n-1=32，由此求得n的值．
（Ⅱ）在所给的等式中，令x=0，可得a0=1．再令x=1可得a0+a1+a2+a3+…+a6=1，从而求得a1+a2+a3+…+an =a1+a2+a3+…+a6 的值．
（Ⅱ）在所给的等式中，令x=0，可得a0=1．再令x=1可得a0+a1+a2+a3+…+a6=1，从而求得a1+a2+a3+…+an =a1+a2+a3+…+a6 的值．
解答：
解：（Ⅰ）由题意可得 2n-1=32，∴n=6．
（Ⅱ）∵（1-2x）n=（1-2x）6=a0+a1x+a2x2+…+a6x6 ，
令x=0，可得a0=1．
再令x=1可得a0+a1+a2+a3+…+a6=1，∴a1+a2+a3+…+an =a1+a2+a3+…+a6=0．
（Ⅱ）∵（1-2x）n=（1-2x）6=a0+a1x+a2x2+…+a6x6 ，
令x=0，可得a0=1．
再令x=1可得a0+a1+a2+a3+…+a6=1，∴a1+a2+a3+…+an =a1+a2+a3+…+a6=0．
点评：本题主要考查二项式定理的应用，是给变量赋值的问题，关键是根据要求的结果，选择合适的数值代入，属于基题．
练习册系列答案
相关题目
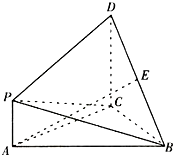如图，△ABC是等边三角形，PA⊥平面ABC，DC∥PA，且DC=AC=2PA=2，E是BD的中点．