题目内容

甲、乙两射手独立地进行射击，设甲击中靶的概率为0.9，乙击中靶的概率为0.8，试求下列条件的概率；
（1）甲乙两人都中靶的概率；
（2）甲、乙两人至少有1人中靶的概率．
考点：相互独立事件的概率乘法公式,互斥事件的概率加法公式
专题：概率与统计
分析：（1）在一次射击中，甲、乙同时射中目标的概率为单独射中目标时的概率之积计算．
（2）根据互斥的概率，甲、乙两人至少有1人中靶的概率的对立事件为甲乙都不中．
解答： 解：（1）∵甲射中目标的概率为0.9，乙射中目标的概率为0.8，
∴甲、乙同时射中目标的概率是0.9×0.8=0.72．
（2）甲、乙两人至少有1人中靶的概率，包括甲、乙两人都中靶，甲中靶乙不中靶，甲不中靶乙中靶，对立事件是他们都不中，
根据互斥事件的概率计算公式得甲、乙两人至少有1人中靶的概率P=1-（1-0.9）（1-0.8）=0.98
点评：本题利用了概率的性质求解．用到的知识点为：两步完成的事件的概率=第一步事件的概率与第二步事件的概率的积．
练习册系列答案
相关题目
已知sin（π-α）=
3
5
，α∈（
π
2
，π）．
（1）求cos（π+α）的值；
（2）求tan（π-α）的值；
（3）求sin2α+cos2α的值．
设函数f（x）=x3-6x+5，x∈R
（1）求f（x）的单调区间和极值；
（2）若直线y=a与y=f（x）的图象有三个不同的交点，求实数a的取值范围；
（3）已知当x∈（1，+∞）时，f（x）≥k（x-1）恒成立，求实数k的取值范围．
若实数x，y，m满足|x-m|＞|y-m|，则称x比y远离m．
（Ⅰ）若x-1比1远离0，求x的取值范围；
（Ⅱ）对任意两个不相等的正数a，b，证明：
a2+b2
2
比（
a+b
2
）2远离0．
设圆（x+1）2+y2=16的圆心为C，A（1，0）是圆内一点，Q为圆周上任意一点，线段AQ的垂直平分线与CQ的连线交于点M．
（1）求点M的轨迹T的方程；
（2）设直线l：y=kx+1-2k恒过点P，且与曲线T相交于不同的两点B、D，若
PB
•
PD
＞
5
4
，试求k的取值范围．
NBA（美国职业篮球联赛）决赛实行7局制，比赛先胜4局者获得比赛的胜利（每局比赛都必须分出胜负，没有平局），比赛随即结束．除第七局甲队获胜的概率是
1
2
外，其余每局比赛甲队获胜的概率都是
2
3
，假设各局比赛结果相互独立．
（1）求甲队以4：0获得胜利的概率；
（2）若每局比赛胜利方得1分，对方得0分，求乙队最终比赛总得分X的分布列及数学期望．
设
a
=（cosx，sinx），
b
=（cosx，
3
cosx），f（x）=
a
•
b
，x∈R．
（1）求f（x）的单调递增区间；
（2）当x∈[0，
π
2
]时，求f（x）的值域．
函数y=sin（
π
2
+x）cos（
π
6
-x）的最小正周期为
 
．
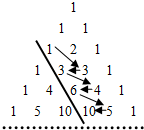如图，在杨辉三角中，斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}：1，3，3，4，6，5，10，…，记其前n项和为Sn，则S27的值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网