题目内容
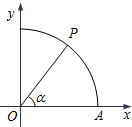 如图,曲线Γ:x2+y2=1(x≥0,y≥0)与x轴交于点A,点P在曲线Γ上,∠AOP=α.
如图,曲线Γ:x2+y2=1(x≥0,y≥0)与x轴交于点A,点P在曲线Γ上,∠AOP=α.(Ⅰ)若点P的坐标是(
| 3 |
| 5 |
| 4 |
| 5 |
| α |
| 2 |
| α |
| 2 |
| α |
| 2 |
(Ⅱ)求函数f(α)=sin(α-
| π |
| 6 |
| 3 |
| π |
| 6 |
考点:三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:(1)根据P点坐标,分别求得sinα和cosα的值,最后利用二倍角公式整理所求,代入即可.
(2)利用两角和公式对函数解析式整理,根据α的范围确定函数的最大和最小值.
(2)利用两角和公式对函数解析式整理,根据α的范围确定函数的最大和最小值.
解答:
解:(1)依题意知sinα=
,cosα=
,
∴2cos
(cos
+sin
)=2cos2
+2sin
cos
=cosα+sinα+1=
+
+1=2.
(2)f(α)=sin(α-
)+
cos(α-
)=2sin(α-
+
)=2sin(α+
),
∵0≤α≤
,
∴
≤α+
≤
∴
≤sin(α+
)≤1
∴1≤f(x)≤2,即函数的值域为[1,2]
| 4 |
| 5 |
| 3 |
| 5 |
∴2cos
| α |
| 2 |
| α |
| 2 |
| α |
| 2 |
| α |
| 2 |
| α |
| 2 |
| α |
| 2 |
| 3 |
| 5 |
| 4 |
| 5 |
(2)f(α)=sin(α-
| π |
| 6 |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
∵0≤α≤
| π |
| 2 |
∴
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
∴
| 1 |
| 2 |
| π |
| 6 |
∴1≤f(x)≤2,即函数的值域为[1,2]
点评:本题主要考查了两角和公式和二倍角公式的化简求值,三角函数图象与性质.考查了学生对三角函数基础知识的综合掌握.

练习册系列答案
相关题目
从伦敦奥运会的一张贵宾票和两张普通票中随机抽取一张,抽到贵宾票的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
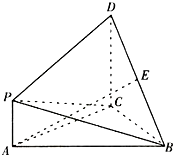 如图,△ABC是等边三角形,PA⊥平面ABC,DC∥PA,且DC=AC=2PA=2,E是BD的中点.
如图,△ABC是等边三角形,PA⊥平面ABC,DC∥PA,且DC=AC=2PA=2,E是BD的中点.