题目内容
双曲线
-
=1(a>0,b>0)与椭圆
+
=1有相同的焦点F1,F2,且该双曲线的渐近线方程为y=±
x.
(1)求双曲线的标准方程;
(2)过该双曲线的右焦点F2作斜率不为零的直线与此双曲线的左,右两支分别交于点m、n,设
=λ
,当x轴上的点G满足
⊥(
-λ
)时,求点G的坐标.
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 9 |
| y2 |
| 5 |
| 3 |
(1)求双曲线的标准方程;
(2)过该双曲线的右焦点F2作斜率不为零的直线与此双曲线的左,右两支分别交于点m、n,设
| MF2 |
| F2N |
| F1F2 |
| GM |
| GN |
考点:双曲线的简单性质
专题:向量与圆锥曲线,圆锥曲线的定义、性质与方程
分析:(1)根据焦点和渐近线方程求其标准方程即可;
(2)设出直线方程,直线方程和双曲线方程联立,利用向量的关系,即可求得.
(2)设出直线方程,直线方程和双曲线方程联立,利用向量的关系,即可求得.
解答:
解:(1)由题可知:
=
,c=2,c2=a2+b2,解得a2=1.b2=1,
所求双曲线方程为 x2-
=1…(5分)
(2)设过点F2的直线方程为:x=ky+2,
联立方程组
,消去x得:(3k2-1)y2+12ky+9=0,
设M(x1,y1),N(x2,y2),则
①…(7分)
由
=λ
得:λ=-
,②
设G(t,0),由
=(4,0),及
⊥(
-λ
)得:
(x1-t-λx2+λt,y1-λy2)•(4,0),即x1-t-λx2+λt=0,③…(10分)
由②,③得ky1+2-t+
(ky2+2)-
t=0,
代入上述条件得:t=
,即G(
,0).…(13分)
| b |
| a |
| 3 |
所求双曲线方程为 x2-
| y2 |
| 3 |
(2)设过点F2的直线方程为:x=ky+2,
联立方程组
|
设M(x1,y1),N(x2,y2),则
|
由
| MF2 |
| F2N |
| y1 |
| y2 |
设G(t,0),由
| F1F2 |
| F1F2 |
| GM |
| GN |
(x1-t-λx2+λt,y1-λy2)•(4,0),即x1-t-λx2+λt=0,③…(10分)
由②,③得ky1+2-t+
| y1 |
| y2 |
| y1 |
| y2 |
代入上述条件得:t=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查双曲线的性质和标准方程,直线与双曲线的相交,向量的应用.

练习册系列答案
相关题目
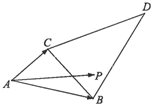
如图,△BCD与△ABC的面积之比为2,点P是区域ABCD内任意一点(含边界),且
=λ
+μ
(λ,μ∈R),则λ+μ的取值范围是( )
| AP |
| AB |
| AC |

| A、[0,1] |
| B、[0,2] |
| C、[0,3] |
| D、[0,4] |
函数y=log3x-
的零点大约所在区间为( )
| 2 |
| x+1 |
| A、(1,2) |
| B、(2,3) |
| C、(3,4) |
| D、(4,5) |