题目内容
若|x+a|-|x-4|≤5-|a+1|(x∈R)恒成立.求实数a的取值范围.
考点:函数恒成立问题
专题:函数的性质及应用
分析:利用绝对值三角不等式求出f(x)的最大值,可得f(x)的最大值小于或等于5-|a+1|,解绝对值不等式,求得a的范围.
解答:
解:因为f(x)=|x+a|-|x-4|=|x+a|-|4-x|≤|(x+a)+(4-x)|=|a+4|,
要使f(x)≤5-|a+1|恒成立,须使|a+4|≤5-|a+1|,
即|a+4|+|a+1|≤5,∴
①,或
②,或
③.
解①求得-5≤a<-4,解②求得-4≤a<-1,解③求得-1≤a≤0,
综合可得a的范围是[-5,0].
要使f(x)≤5-|a+1|恒成立,须使|a+4|≤5-|a+1|,
即|a+4|+|a+1|≤5,∴
|
|
|
解①求得-5≤a<-4,解②求得-4≤a<-1,解③求得-1≤a≤0,
综合可得a的范围是[-5,0].
点评:本题主要考查带由绝对值的函数,绝对值不等式的解法,函数恒成立问题的应用,体现了转化、分类讨论的数学思想,属于中档

练习册系列答案
相关题目
设集合A={4,5,6,8},B={3,5,7,8},则A∪B中元素的个数为( )
| A、5 | B、6 | C、7 | D、8 |
若函数f(x)=(x-1)(x-3)+(x-3)(x-4)+(x-4)(x-1),则函数f(x)的两个零点分别位于区间( )
| A、(1,3)和(3,4)内 |
| B、(-∞,1)和(1,3)内 |
| C、(3,4)和(4,+∞)内 |
| D、(-∞,1)和(4,+∞)内 |
对于实数m,n定义运算“⊕”:m⊕n=
,设f(x)=(2x-1)⊕(x-1),且关于x的方程f(x)=a恰有三个互不相等的实数根x1,x2,x3,则x1x2x3的取值范围是( )
|
A、(-
| ||
B、(-
| ||
C、(0,
| ||
D、(0,
|
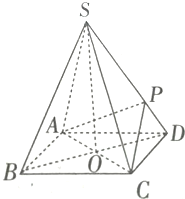 如图所示,四棱锥S-ABCD的底面是正方形,每条侧棱长都是底面边长的
如图所示,四棱锥S-ABCD的底面是正方形,每条侧棱长都是底面边长的