题目内容
7.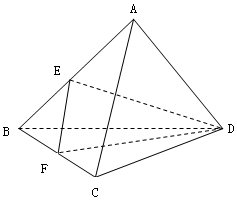 如图,已知正三棱锥A-BCD中,E、F分别是棱AB、BC的中点,EF⊥DE,且BC=2.
如图,已知正三棱锥A-BCD中,E、F分别是棱AB、BC的中点,EF⊥DE,且BC=2.(1)求此正三棱锥的体积;
(2)求DE与平面ABC所成角的余弦值.
分析 (1)由题意判定正三棱锥的形状,三条侧棱两两垂直,推出是正方体的一个角,然后转化顶点和底面从而求其体积.
(2)由(1)可知DA⊥平面ABC,∠DEA是DE与平面ABC所成角,即可求DE与平面ABC所成角的余弦值.
解答 解:(1)∵EF∥AC,EF⊥DE,
∴AC⊥DE,
∵AC⊥BD(正三棱锥性质),
∴AC⊥平面ABD 所以正三棱锥A-BCD是正方体的一个角,
∵BC=2,
∴AB=$\sqrt{2}$,
∴V=$\frac{1}{3}×\frac{1}{2}×\sqrt{2}×\sqrt{2}×\sqrt{2}$=$\frac{\sqrt{2}}{3}$;
(2)由(1)可知DA⊥平面ABC,∴∠DEA是DE与平面ABC所成角,
∵tan∠DEA=2,∴cos∠DEA=$\frac{\sqrt{5}}{5}$.
点评 本题考查棱锥的体积,考查线面角,考查逻辑思维能力,空间想象能力,是基础题.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
19.已知M (-2,0),N (2,0),则以MN为直径的圆的方程是( )
| A. | x2+y2=2 | B. | x2+y2=1 | C. | x2+y2=3 | D. | x2+y2=4 |
2.已知函数$f(x)=\left\{\begin{array}{l}|{{{log}_4}x}|,\;0<x≤4\\{x^2}-10x+25,\;x>4.\end{array}\right.$若a,b,c,d是互不相同的正数,且f(a)=f(b)=f(c)=f(d),则abcd的取值范围是( )
| A. | (24,25) | B. | (18,24) | C. | (21,24) | D. | (18,25) |
12.命题“存在x0∈R+,使log2x0≤0”的否定是( )
| A. | 不存在x0∈R+,使log2x0>0 | B. | 对任意的x∈R+,有log2x>0 | ||
| C. | 对任意的x∈R+,有log2x≤0 | D. | 存在x0∈R+,使log2x0>0 |
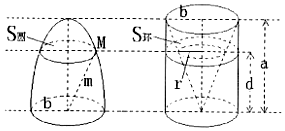 已知两个等高的几何体在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.椭球体是椭圆绕其轴旋转所成的旋转体.如图将底面直径皆为2b,高皆为a的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面β上.以平行于平面β的平面于距平面β任意高d处可横截得到S圆及S环两截面,可以证明S圆=S环总成立.则短轴长为4cm,长轴为6cm的椭球体的体积为16πcm3.
已知两个等高的几何体在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.椭球体是椭圆绕其轴旋转所成的旋转体.如图将底面直径皆为2b,高皆为a的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面β上.以平行于平面β的平面于距平面β任意高d处可横截得到S圆及S环两截面,可以证明S圆=S环总成立.则短轴长为4cm,长轴为6cm的椭球体的体积为16πcm3.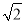 B.4
B.4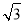 C.4
C.4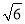 D.
D.
 的是( )
的是( )


