题目内容
19.已知$sinα+cosα=\frac{1}{5}$,求:(1)sinα-cosα的值;
(2)若α是△ABC的内角,判断△ABC的形状.
分析 (1)根据同角三角函数关系式即可求解.
(2)根据sinα、cosα的值判断即可.
解答 解:由$sinα+cosα=\frac{1}{5}$,可得:1+2sinαcosα=$\frac{1}{25}$
得:2sinαcosα=$-\frac{24}{25}$
令sinα-cosα=M,则1-2sinαcosα=M2.
故得:M=$±\frac{7}{5}$.
(2)由$sinα+cosα=\frac{1}{5}$,sin2α+cos2α=1,解得:$\left\{\begin{array}{l}{sinα=\frac{4}{5}}\\{cosα=-\frac{3}{5}}\end{array}\right.$或$\left\{\begin{array}{l}{sinα=-\frac{3}{5}}\\{cosα=\frac{4}{5}}\end{array}\right.$
∵α是△ABC的内角
∴$\left\{\begin{array}{l}{sinα=\frac{4}{5}}\\{cosα=-\frac{3}{5}}\end{array}\right.$,∴$α∈(\frac{π}{2},π)$
∴△ABC时钝角三角形.
点评 本题考查了同角三角函数基本关系式,考查了计算能力,属于基础题.

练习册系列答案
相关题目
14.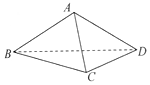 如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,直线AC与底面BCD所成角的大小为( )
如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,直线AC与底面BCD所成角的大小为( )
 如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,直线AC与底面BCD所成角的大小为( )
如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,直线AC与底面BCD所成角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
3.函数f(x)=$\left\{\begin{array}{l}{lnx(x>0)}\\{-\sqrt{-x}(x≤0)}\end{array}\right.$与g(x)=$\frac{1}{2}$(|x+a|+1)的图象上存在关于y轴对称的点,则实数a的取值范围是( )
| A. | (-∞,3-2ln2] | B. | [3-2ln2,+∞) | C. | [$\sqrt{e}$,+∞) | D. | (-∞,$-\sqrt{e}$] |
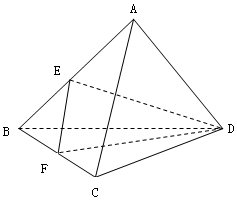 如图,已知正三棱锥A-BCD中,E、F分别是棱AB、BC的中点,EF⊥DE,且BC=2.
如图,已知正三棱锥A-BCD中,E、F分别是棱AB、BC的中点,EF⊥DE,且BC=2. 的解集为
的解集为 .则
.则 ( )
( ) B.
B. C.
C. D.
D.