题目内容
16.设A是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{a}^{2}-4}$=1(a>0)上的动点,点F的坐标为(-2,0),若满足|AF|=10的点A有且仅有两个,则实数a的取值范围为8<a<12.分析 由题意,F是椭圆的焦点,满足|AF|=10的点A有且仅有两个,可得a-2<10<a+2,即可得出结论.
解答 解:由题意,F是椭圆的焦点,
∵满足|AF|=10的点A有且仅有两个,
∴a-2<10<a+2,
∴8<a<12,
故答案为:8<a<12.
点评 本题考查椭圆的方程与性质,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
20.已知函数f(x)=2x+x2-xln2-2,若函数g(x)=|f(x)|-loga(x+2)(a>1)在区间[-1,1]上有4个不同的零点,则实数a的取值范围是( )
| A. | (1,2) | B. | (2,+∞) | C. | [3${\;}^{\frac{1}{1-ln2}}$,+∞) | D. | (2,3${\;}^{\frac{1}{1-ln2}}$] |
3.函数f(x)=$\left\{\begin{array}{l}{lnx(x>0)}\\{-\sqrt{-x}(x≤0)}\end{array}\right.$与g(x)=$\frac{1}{2}$(|x+a|+1)的图象上存在关于y轴对称的点,则实数a的取值范围是( )
| A. | (-∞,3-2ln2] | B. | [3-2ln2,+∞) | C. | [$\sqrt{e}$,+∞) | D. | (-∞,$-\sqrt{e}$] |
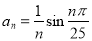 ,
,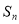 是
是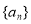 的前
的前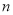 项和.在
项和.在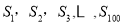 中,正数的个数是( )
中,正数的个数是( )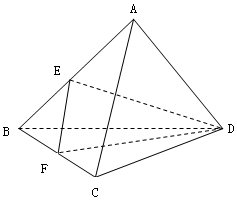 如图,已知正三棱锥A-BCD中,E、F分别是棱AB、BC的中点,EF⊥DE,且BC=2.
如图,已知正三棱锥A-BCD中,E、F分别是棱AB、BC的中点,EF⊥DE,且BC=2. 满足
满足 ,数列
,数列 是等比数列,且
是等比数列,且 , 则
, 则 的值等于 .
的值等于 .