题目内容
19.已知M (-2,0),N (2,0),则以MN为直径的圆的方程是( )| A. | x2+y2=2 | B. | x2+y2=1 | C. | x2+y2=3 | D. | x2+y2=4 |
分析 根据中点坐标公式算出MN的中点坐标为(0,0),且|MN|=4,从而得到所求圆的圆心为原点、半径r=2,可得圆的标准方程.
解答 解:∵点(-2,0),N (2,0),
∴线段MN的中点坐标为(0,0),且|MN|=4.
因此,以线段MN为直径的圆,它的圆心为(0,0),半径r=2,
∴圆的方程为x2+y2=4.
故选:D.
点评 本题给出M、N两点的坐标,求以AB为直径的圆的方程.着重考查了线段中点坐标公式、两点间的距离公式和圆的标准方程等知识,属于基础题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
14.已知集合M={y|y=2x,x>0},N={x|2x-x2≥0},则M∩N为( )
| A. | (1,2] | B. | (1,2) | C. | [2,+∞) | D. | [1,+∞) |
4.已知圆的半径为πcm,则120°的圆心角所对的弧长是( )
| A. | $\frac{π}{3}$cm | B. | $\frac{{π}^{2}}{3}$cm | C. | $\frac{2π}{3}$cm | D. | $\frac{2{π}^{2}}{3}$cm |
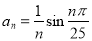 ,
,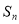 是
是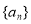 的前
的前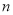 项和.在
项和.在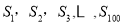 中,正数的个数是( )
中,正数的个数是( )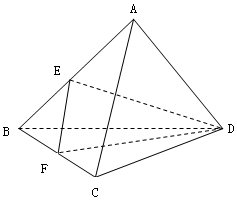 如图,已知正三棱锥A-BCD中,E、F分别是棱AB、BC的中点,EF⊥DE,且BC=2.
如图,已知正三棱锥A-BCD中,E、F分别是棱AB、BC的中点,EF⊥DE,且BC=2.