题目内容
2.已知函数$f(x)=\left\{\begin{array}{l}|{{{log}_4}x}|,\;0<x≤4\\{x^2}-10x+25,\;x>4.\end{array}\right.$若a,b,c,d是互不相同的正数,且f(a)=f(b)=f(c)=f(d),则abcd的取值范围是( )| A. | (24,25) | B. | (18,24) | C. | (21,24) | D. | (18,25) |
分析 画出函数y=f(x)的图象,运用对数函数的图象,结合对数运算性质,可得ab=1,由二次函数的性质可得c+d=10,运用基本不等式和二次函数的性质,即可得到所求范围.
解答  解:先画出函数$f(x)=\left\{\begin{array}{l}|{{{log}_4}x}|,\;0<x≤4\\{x^2}-10x+25,\;x>4.\end{array}\right.$的图象,如图:
解:先画出函数$f(x)=\left\{\begin{array}{l}|{{{log}_4}x}|,\;0<x≤4\\{x^2}-10x+25,\;x>4.\end{array}\right.$的图象,如图:
∵a,b,c,d互不相同,不妨设a<b<c<d.
且f(a)=f(b)=f(c)=f(d),
而-log4a=log4b,即有log4a+log4b=0,
可得ab=1,
则abcd=cd,
由c+d=10,可得cd<($\frac{c+d}{2}$)2=25,
且cd=c(10-c)=-(c-5)2+25,
当c=4时,d=6,cd=24,但此时b,c相等,
故ab的范围为(24,25).
故选:A.
点评 本题考查了利用函数图象分析解决问题的能力,以及对数函数图象的特点,注意体会数形结合思想在本题中的运用.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
14.已知集合M={y|y=2x,x>0},N={x|2x-x2≥0},则M∩N为( )
| A. | (1,2] | B. | (1,2) | C. | [2,+∞) | D. | [1,+∞) |
14.已知a=${∫}_{0}^{1}$(x2-1)dx,b=1-log23,c=cos$\frac{5π}{6}$,则a,b,c的大小关系是( )
| A. | a<b<c | B. | c<a<b | C. | a<c<b | D. | b<c<a |
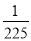 B.
B.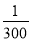 C.
C.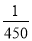 D.以上全不对
D.以上全不对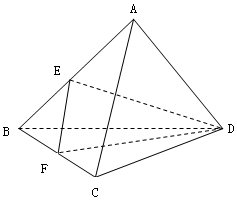 如图,已知正三棱锥A-BCD中,E、F分别是棱AB、BC的中点,EF⊥DE,且BC=2.
如图,已知正三棱锥A-BCD中,E、F分别是棱AB、BC的中点,EF⊥DE,且BC=2.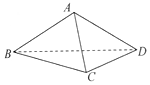 如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,直线AC与底面BCD所成角的大小为( )
如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,直线AC与底面BCD所成角的大小为( ) 的解集为
的解集为 .则
.则 ( )
( ) B.
B. C.
C. D.
D.
 ,那么cosC等于 ( )
,那么cosC等于 ( ) B.
B. C.
C. D.
D.