题目内容
已知函数f(x)=sin(x-
)(x∈R),下面命题中,真命题是 .
(1)函数f(x)的最小正周期为2π;
(2)函数f(x)在区间[0,
]上是增函数;
(3)函数f(x)的图象关于直线x=0对称;
(4)函数f(x)是奇函数;
(5)函数f(x)的图象是将y=sinx向左平移
个单位得到的.
| π |
| 2 |
(1)函数f(x)的最小正周期为2π;
(2)函数f(x)在区间[0,
| π |
| 2 |
(3)函数f(x)的图象关于直线x=0对称;
(4)函数f(x)是奇函数;
(5)函数f(x)的图象是将y=sinx向左平移
| π |
| 2 |
考点:命题的真假判断与应用,三角函数的周期性及其求法,复合三角函数的单调性
专题:三角函数的图像与性质
分析:先利用诱导公式将函数化简为y=-cosx,然后根据余弦函数的图象和性质判定即可.
解答:
解:函数f(x)=sin(x-
)=-sin(
-x)=-cosx,
①函数f(x)的最小正周期为2π;(1)正确;
②在区间[0,
]上,函数y=cosx是减函数,则y=-cosx为增函数,(2)正确,
③函数为偶函数,则函数f(x)的图象关于直线x=0对称,(3)正确,
④函数f(x)是偶函数,(4)错误,
⑤左加右减,函数f(x)的图象是将y=sinx向右平移
个单位得到的,(5)错误,
故答案为:(1)(2)(3)
| π |
| 2 |
| π |
| 2 |
①函数f(x)的最小正周期为2π;(1)正确;
②在区间[0,
| π |
| 2 |
③函数为偶函数,则函数f(x)的图象关于直线x=0对称,(3)正确,
④函数f(x)是偶函数,(4)错误,
⑤左加右减,函数f(x)的图象是将y=sinx向右平移
| π |
| 2 |
故答案为:(1)(2)(3)
点评:本题考察三角函数的基本性质以及诱导公式,属于基础题目,解题的关键是对于三角的图象和性质的熟练把握.

练习册系列答案
相关题目
函数y=loga(3x-1)(a>0,a≠1)的图象过定点( )
A、(
| ||
| B、(-1,0) | ||
C、(
| ||
| D、(0,-1) |
某银行准备新设一种定期存款业务,经预测,存款量与存款利率成正比,比例系数为k (k>0),贷款的利率为4.8%,假设银行吸收的存款能全部放贷出去.若存款利率为x(x∈(0,0.048)),则存款利率为多少时,银行可获得最大利益( )
| A、0.012 |
| B、0.024 |
| C、0.032 |
| D、0.036 |
若函数f(x)=|ax|-x-a(a>0)有两个零点,则a的取值范围是( )
| A、(1,+∞) | B、(0,1) |
| C、(0,+∞) | D、∅ |
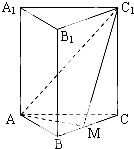 如图,正三棱柱ABC-A1B1C1的底面边长为1,点M在BC上,△AMC1是以M为直角顶点的等腰直角三角形.
如图,正三棱柱ABC-A1B1C1的底面边长为1,点M在BC上,△AMC1是以M为直角顶点的等腰直角三角形.