题目内容
若函数f（x）=|ax|-x-a（a＞0）有两个零点，则a的取值范围是（ ）
| A、（1，+∞） | B、（0，1） |
| C、（0，+∞） | D、∅ |
考点：函数零点的判定定理
专题：计算题,函数的性质及应用
分析：f（x）=|ax|-x-a=
，函数f（x）=|ax|-x-a（a＞0）有两个零点转化为方程f（x）=0有两个根．
|
解答：
解：f（x）=|ax|-x-a=
，
∵令f（x）=0得，
x=
＞0，x=
＜0，
解得，a＞1，
故选A．
|
∵令f（x）=0得，
x=
| a |
| a-1 |
| a |
| -a-1 |
解得，a＞1，
故选A．
点评：本题考查了函数的零点与方程的根的关系及分段函数求解，属于基础题．
练习册系列答案
相关题目
设P为曲线C：y=x2+2x+3上点，且曲线C在点P处切线倾斜角的取值范围为[0，
]，则点P横坐标的取值范围为（ ）
| π |
| 4 |
A、[
| ||
| B、[-1，0] | ||
| C、[0，1] | ||
D、[-1，-
|
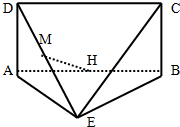已知平面ABCD⊥平面ABE，四边形ABCD是矩形，AD=AE=BE=2，M、H分别是DE、AB的中点，主（正）视图方向垂直平面ABCD时，左（侧）视图的面积为在极坐标系中，直线ρcosθ-ρsinθ-3=0与圆ρ=2cosθ的位置关系是（ ）
| A、相交但不过圆心 | B、相交且过圆心 |
| C、相离 | D、相切 |