题目内容
13．点A（2，0）到直线l：y=x+2的距离为（ ）| A． | $\frac{\sqrt{2}}{2}$ | B． | $\sqrt{2}$ | C． | 2 | D． | 2$\sqrt{2}$ |
分析 化直线方程为一般式，然后直接利用点到直线的距离公式求解．
解答 解：由l：y=x+2，得x-y+2=0，所以点（2，0）到直线x-y+2=0的距离为d=$\frac{4}{\sqrt{2}}$=2$\sqrt{2}$．
故选：D．
点评 本题考查了点到直线的距离公式，是基础的运算题．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
14．已知实数x，y满足$\left\{\begin{array}{l}x+y-4≤0\\ x-y≤0\\ x≥1\end{array}\right.$，则z=2x+3y的最大值为（ ）
| A． | 5 | B． | 8 | C． | 10 | D． | 11 |
1．命题p：?x0≥2，x02-2x0-2＞0的否定是（ ）
| A． | ?x0≥2，x02-2x0-2＜0 | B． | ?x0＜2，x02-2x0-2＜0 | ||
| C． | ?x＜2，x2-2x-2≤0 | D． | ?x≥2，x2-2x-2≤0 |
8．某校高三共有2000名学生参加广安市联考，现随机抽取100名学生的成绩单（单位：分），并列成如表所示的频数分布表：
（1）试估计该年级成绩≥80分的学生人数；
（2）已知样本在成绩在[40，50）中的6名学生中，有4名男生，2名女生，现从中选2人进行调研，求恰好选中一名男生一名女生的概率．
| 组别 | [40，50） | [50，60） | [60，70） | [70，80） | [80，90） | [90，100] |
| 频数 | 6 | 18 | 28 | 26 | 17 | 5 |
（2）已知样本在成绩在[40，50）中的6名学生中，有4名男生，2名女生，现从中选2人进行调研，求恰好选中一名男生一名女生的概率．
18．若集合A={x|x＜3}，B={x|x＞0}，则A∪B=（ ）
| A． | {x|0＜x＜3} | B． | {x|x＞0} | C． | {x|x＜3} | D． | R |
2．2016年是红色长征胜利80周年，某市电视台举办纪念红军长征胜利80周年知识问答，宣传长征精神，首先在甲、乙、丙、丁四个不同的公园进行支持签名活动
然后在各公园签名的人中按分层抽样的方式抽取10名幸运之星回答问题，从10个关于长征的问题中随机抽取4个问题让幸运之星回答，全部答对的幸运之星获得一份纪念品．
（Ⅰ）求此活动轴个各公园幸运之星的人数
（Ⅱ）若乙公园中每位幸运之星对每个问题答对的概率均为$\frac{\sqrt{2}}{2}$，求恰好2位幸运之星获得纪念品的概率
（Ⅲ）若幸运之星小李对其中8个问题能答对，而另外2个问题答不对，记小李答对的问题数为X，求X的分布列及数学期望E（X）
| 公园 | 甲 | 乙 | 丙 | 丁 |
| 获得签名人数 | 45 | 60 | 30 | 15 |
（Ⅰ）求此活动轴个各公园幸运之星的人数
（Ⅱ）若乙公园中每位幸运之星对每个问题答对的概率均为$\frac{\sqrt{2}}{2}$，求恰好2位幸运之星获得纪念品的概率
（Ⅲ）若幸运之星小李对其中8个问题能答对，而另外2个问题答不对，记小李答对的问题数为X，求X的分布列及数学期望E（X）
3．如图，在网格中粗线显示的为某几何体的三视图（正方形网格的边长为1），则该几何体的体积为（ ）
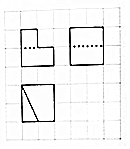
| A． | 5 | B． | 6 | C． | 6.5 | D． | 7 |