题目内容
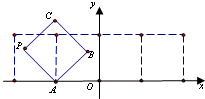 如图放置的边长为1的正方形PABC沿x轴滚动,点B恰好经过原点.设顶点P(x,y)的轨迹方程是y=f(x),则对函数y=f(x)有下列判断:
如图放置的边长为1的正方形PABC沿x轴滚动,点B恰好经过原点.设顶点P(x,y)的轨迹方程是y=f(x),则对函数y=f(x)有下列判断:①函数y=f(x)是偶函数;
②对任意的x∈R,都有f(x+2)=f(x-2);
③函数y=f(x)在区间[2,3]上单调递减;
④函数y=f(x)在区间[4,6]上是减函数.
其中判断正确的序号是
考点:命题的真假判断与应用,函数的图象
专题:函数的性质及应用,简易逻辑
分析:根据正方形的运动,得到点P的轨迹方程,然后根据函数的图象和性质分别进行判断即可.
解答:
 解:当-2≤x≤-1,P的轨迹是以A为圆心,半径为1的
解:当-2≤x≤-1,P的轨迹是以A为圆心,半径为1的
圆,
当-1≤x≤1时,P的轨迹是以B为圆心,半径为
的
圆,
当1≤x≤2时,P的轨迹是以C为圆心,半径为1的
圆,
当3≤x≤4时,P的轨迹是以A为圆心,半径为1的
圆,
∴函数的周期是4.
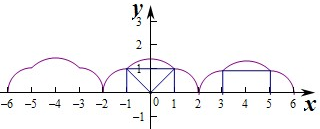
因此最终构成图象如下:
①根据图象的对称性可知函数y=f(x)是偶函数,∴①正确.
②由图象即分析可知函数的周期是4.∴②正确.
③函数y=f(x)在区间[2,3]上单调递增,∴③错误.
④函数y=f(x)在区间[4,6]上是减函数,由函数的图象即可判断是真命题、∴④正确.
故答案为:①②④.
 解:当-2≤x≤-1,P的轨迹是以A为圆心,半径为1的
解:当-2≤x≤-1,P的轨迹是以A为圆心,半径为1的| 1 |
| 4 |
当-1≤x≤1时,P的轨迹是以B为圆心,半径为
| 2 |
| 1 |
| 4 |
当1≤x≤2时,P的轨迹是以C为圆心,半径为1的
| 1 |
| 4 |
当3≤x≤4时,P的轨迹是以A为圆心,半径为1的
| 1 |
| 4 |
∴函数的周期是4.
因此最终构成图象如下:
①根据图象的对称性可知函数y=f(x)是偶函数,∴①正确.
②由图象即分析可知函数的周期是4.∴②正确.
③函数y=f(x)在区间[2,3]上单调递增,∴③错误.
④函数y=f(x)在区间[4,6]上是减函数,由函数的图象即可判断是真命题、∴④正确.
故答案为:①②④.
点评:本题考查的知识点是函数图象的变化,其中根据已知画出正方形转动过程中的一个周期内的图象,利用数形结合的思想对本题进行分析是解答本题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
若变量x,y满足约束条件
,则z=4y-x的最大值为( )
|
| A、12 | B、16 | C、0 | D、32 |
已知集合A={x|0<x<2},B={x|y=
},则A∪∁RB=( )
| 1-x2 |
| A、(0,1) |
| B、(1,2) |
| C、(-∞,-1)∪(0,+∞) |
| D、(-∞,-1)∪(1,+∞) |
