题目内容
某公司为了测试某款电脑游戏软件的性能,要举行一种叫“电脑闯关比赛”的有奖活动,在一次“电脑闯关比赛”中,甲、乙两位选手在同等的条件下闯关成功的概率分别为
和
.设甲、乙两位选手手闯关相互独立.
(Ⅰ)求至少有一位选手闯关成功的概率;
(Ⅱ)公司根据以往参赛选手对这项活动支持的程度规定:若甲闯关成功可获得奖励300元,若乙闯关成功可获得奖励250元,求该公司奖励的分布列和数学期望.
| 2 |
| 3 |
| 3 |
| 5 |
(Ⅰ)求至少有一位选手闯关成功的概率;
(Ⅱ)公司根据以往参赛选手对这项活动支持的程度规定:若甲闯关成功可获得奖励300元,若乙闯关成功可获得奖励250元,求该公司奖励的分布列和数学期望.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:简易逻辑
分析:(Ⅰ)运用独立事件同时发生的概率,和对立事件的概率求解,
(Ⅱ)首先分析该公司奖励的数值为:ξ=0,250,300,550,再分别求解概率,列出分布列,求出数学期望.
(Ⅱ)首先分析该公司奖励的数值为:ξ=0,250,300,550,再分别求解概率,列出分布列,求出数学期望.
解答:
解:(Ⅰ)设甲闯关成功的事件为A,乙闯关成功的事件为B,
则P(A)=
,P(B)=
,
∴至少有一位选手闯关成功的概率为:1-(1-
)(1-
)=
,
(Ⅱ)∵该公司奖励的数值为:ξ=0,250,300,550,
∴P(ξ=0)=
×
=
,P(ξ=250)=
×
=
,
P(ξ=300)=
×
=
,P(ξ=550)=
×
=
∴该公司奖励的分布列:
ξ的数学期望0×
+250×
+300×
+550×
=350
则P(A)=
| 2 |
| 3 |
| 3 |
| 5 |
∴至少有一位选手闯关成功的概率为:1-(1-
| 2 |
| 3 |
| 3 |
| 5 |
| 13 |
| 15 |
(Ⅱ)∵该公司奖励的数值为:ξ=0,250,300,550,
∴P(ξ=0)=
| 1 |
| 3 |
| 2 |
| 5 |
| 2 |
| 15 |
| 1 |
| 3 |
| 3 |
| 5 |
| 1 |
| 5 |
P(ξ=300)=
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
| 15 |
| 2 |
| 3 |
| 3 |
| 5 |
| 2 |
| 5 |
∴该公司奖励的分布列:
| ξ | 0 | 250 | 300 | 550 | ||||||||
| p |
|
|
|
|
| 2 |
| 15 |
| 1 |
| 5 |
| 4 |
| 15 |
| 2 |
| 5 |
点评:本题考察了古典概率的求解,分布列,数学期望的求解,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
已知函数f(x)=|xex|,方程f2(x)+tf(x)+1=0(t∈R)有四个不同的实数根,则t的取值范围为( )
A、(-∞,-
| ||
| B、(-∞,-2) | ||
C、(-
| ||
D、(
|
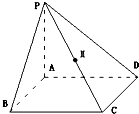 如图,四棱锥P-ABCD中,四边形ABCD是矩形,PA⊥平面ABCD,PA⊥平面ABCD,且PA=
如图,四棱锥P-ABCD中,四边形ABCD是矩形,PA⊥平面ABCD,PA⊥平面ABCD,且PA=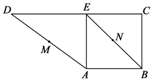 如图,在直角梯形ABCD中,BC⊥DC,AE⊥DC,M、N分别是AD、BE的中点,将三角形ADE沿AE折起,下列说法正确的是
如图,在直角梯形ABCD中,BC⊥DC,AE⊥DC,M、N分别是AD、BE的中点,将三角形ADE沿AE折起,下列说法正确的是