题目内容

设幂函数f（x）=x -m2+2m+3为偶函数，且在区间（0，+∞）为增函数则m
 
．
考点：幂函数图象及其与指数的关系
专题：函数的性质及应用
分析：由于幂函数f（x）=x -m2+2m+3为偶函数，且在区间（0，+∞）为增函数，可得-m2+2m+3＞0，且为偶数．
解答： 解：∵幂函数f（x）=x -m2+2m+3为偶函数，且在区间（0，+∞）为增函数，
∴-m2+2m+3＞0，且为偶数．
解得-1＜m＜3，
∴m=1．
故答案为：1．
点评：本题考查了幂函数的奇偶性与单调性，属于基础题．
练习册系列答案
相关题目
集合M={x|x=2n-2m，n、m∈N}，P={x|1912≤x≤2004}，则M∩P中所有元素的和等于
 
．
已知函数f（x）=lnx+x2．
（1）若函数g（x）=f（x）-ax在定义域内为增函数，求实数a的取值范围；
（2）在（1）的条件下，且a＞1，h（x）=e3x-3aex，x∈[0，ln2]，求h（x）的极小值；
（3）设F（x）=2f（x）-3x2-k（k∈R），若函数F（x）存在两个零点m，n（0＜m＜n），且满足2x0=m+n，问：函数F（x）在（x0，F（x0））处的切线能否平行于x轴？若能，求出该切线方程，若不能，请说明理由．
已知向量
a
=（2，1），
b
=（0，-1），若（
a
-λ
b
）∥
a
，则实数λ=
 
．
已知f（x）是偶函数，且f（x）在[0，+∞）上是增函数，若x∈[
1
2
，1]时，不等式f（1+xlog2a）≤f（x-2）恒成立，则实数a的取值范围是
 
．
一条直线的斜率范围是[-1，
3
]，则这条直线的倾斜角范围是
 
．
函数f（x）=
1
lgx
的定义域是
 
．
设函数f（x）=|x+1|+|x+2|-a（a∈R）
（1）当a=5时，求函数g（x）=lnf（x）的定义域；
（2）若函数h（x）=
f(x)
的定义域为R，试求a的取值范围．
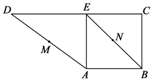如图，在直角梯形ABCD中，BC⊥DC，AE⊥DC，M、N分别是AD、BE的中点，将三角形ADE沿AE折起，下列说法正确的是
 
（填上所有正确的序号）．
①不论D折至何位置（不在平面ABC内）都有MN∥面DEC；
②不论D折至何位置都有MN⊥AE；
③不论D折至何位置（不在平面ABC内）都有MN∥AB．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网