题目内容
在二项式(
+
)10的展开式中,常数项是 .
| x |
| 2 |
| x2 |
考点:二项式系数的性质
专题:计算题,二项式定理
分析:在二项展开式的通项公式中,令x的幂指数等于0,求出r的值,即可求得常数项.
解答:
解:二项式(
+
)10的展开式的通项公式为Tr+1=
•2r•x5-
r,
令5-
r=0,则r=2,
∴常数项是
•22=180,
故答案为:180.
| x |
| 2 |
| x2 |
| C | r 10 |
| 5 |
| 2 |
令5-
| 5 |
| 2 |
∴常数项是
| C | 2 10 |
故答案为:180.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
相关题目
曲线y=e
x在点(4,e2)处的切线与坐标轴所围三角形的面积为( )
| 1 |
| 2 |
| A、e2 | ||
| B、2e2 | ||
| C、4e2 | ||
D、
|
下列式子正确的是( )
A、(
| ||||||||||||
B、
| ||||||||||||
C、|
| ||||||||||||
D、
|
若0>m>n,则下列结论正确的是( )
| A、2m<2n | ||||
B、m+
| ||||
C、log
| ||||
| D、m2<n2 |
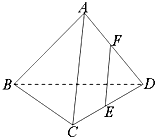 已知在空间四边形ABCD中,AC=AD,BC=BD,且E,F分别是CD,AD的中点.
已知在空间四边形ABCD中,AC=AD,BC=BD,且E,F分别是CD,AD的中点.