题目内容
若0>m>n,则下列结论正确的是( )
| A、2m<2n | ||||
B、m+
| ||||
C、log
| ||||
| D、m2<n2 |
考点:不等式的基本性质
专题:不等式
分析:根据指数函数对数函数幂函数的单调性即可判断
解答:
解:对于A,y=2x为增函数,∵0>m>n,∴2m>2n,故A不正确,
对于B,当m=-
,n=-1时,m+
=-
,n+
=-2,故B不正确,
对于C,y=log
x为减函数,∵0>m>n,∴0<-m<-n,∴log
(-m)>log
(-n),故C不正确,
对于D,y=x2,x∈(-∞,0)上为减函数,∵0>m>n,∴m2<n2,故D正确,
故选:D.
对于B,当m=-
| 1 |
| 2 |
| 1 |
| m |
| 5 |
| 2 |
| 1 |
| n |
对于C,y=log
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
对于D,y=x2,x∈(-∞,0)上为减函数,∵0>m>n,∴m2<n2,故D正确,
故选:D.
点评:本题考查了不等式的性质,利用函数的单调性来判断,是常用的方法,属于基础题

练习册系列答案
相关题目
双曲线
-
=1上一点P到左焦点F1的距离为9,则P到右焦点F2的距离是( )
| x2 |
| 16 |
| y2 |
| 20 |
| A、1 | B、17 |
| C、1或17 | D、23或41 |
方程
+
=1表示焦点在y轴的双曲线,则k的取值范围是( )
| x2 |
| k-3 |
| y2 |
| 2-k |
| A、k<3 | B、k<2 |
| C、2<k<3 | D、k>2 |
函数f(x)=log2(2x)的图象大致是( )
A、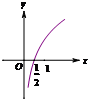 |
B、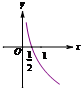 |
C、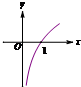 |
D、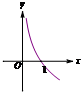 |
执行如图所示的程序框图,则输出的结果为( )


| A、3 | B、4 | C、5 | D、6 |