题目内容
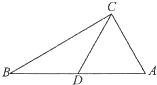如图在△ABC中，已知∠A=| π |
| 3 |
| 3 |
（Ⅰ）若CD=2，S△BDC=2
| 3 |
（Ⅱ）若AC=AD，求△BCD周长的最大值．
考点：余弦定理,正弦定理
专题：计算题,解三角形
分析：（Ⅰ）利用面积公式求得sin∠BCD的值，进而求得∠BCD，然后利用余弦定理求得BD．
（Ⅱ）利用正弦定理分别表示出DC，BD的关系式，进而与BC相加表达出三角形的周长，根据三角函数的性质求得其最大值．
（Ⅱ）利用正弦定理分别表示出DC，BD的关系式，进而与BC相加表达出三角形的周长，根据三角函数的性质求得其最大值．
解答：
．解：（Ⅰ）∵S△BDC=
BC•CD•sin∠BCD=2
，
∴sin∠BCD=
∴∠BCD=
∵在△BCD中，由余弦定理得BD2=BC2+CD2-2BD•CD•cos∠BCD=4+48-2×2×4
×
=28，
∴BD=2
．
（Ⅱ）∵AC=AD，∠A=
，
∴△ACD为正三角形，
在△BCD中，由正弦定理得
=
=
=8
∴DC=8sinB，BD=8sin（
-B），
∴△BCD周长为BD+DC+BC=4
+8sinB+8sin（
-B）=8sin（B+
）+4
，
∵∠BDC=
，
∴0＜∠B＜
，
∴
＜∠B+
＜
，
∴当∠B+
=
，即∠B=
时，
△BDC周长取得最大值，最大值为8+4
．
| 1 |
| 2 |
| 3 |
∴sin∠BCD=
| 1 |
| 2 |
∴∠BCD=
| π |
| 6 |
∵在△BCD中，由余弦定理得BD2=BC2+CD2-2BD•CD•cos∠BCD=4+48-2×2×4
| 3 |
| ||
| 2 |
∴BD=2
| 7 |
（Ⅱ）∵AC=AD，∠A=
| π |
| 3 |
∴△ACD为正三角形，
在△BCD中，由正弦定理得
| DC |
| sinB |
| BD | ||
sin(
|
| BC |
| sin∠BDC |
∴DC=8sinB，BD=8sin（
| π |
| 3 |
∴△BCD周长为BD+DC+BC=4
| 3 |
| π |
| 3 |
| π |
| 3 |
| 3 |
∵∠BDC=
| 2π |
| 3 |
∴0＜∠B＜
| π |
| 3 |
∴
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴当∠B+
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
△BDC周长取得最大值，最大值为8+4
| 3 |
点评：本题主要考查了正弦定理和余弦定理的运用．考查了基础知识的综合运用．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
命题“若m＞0，则关于x的方程x2+x-m=0有实数根”的逆否命题为（ ）
| A、若关于x的方程x2+x-m=0未找到引用源．有实数根，则m≤0 |
| B、若m≤0，则关于x的方程x2+x-m=0没有实数根 |
| C、若关于x的方程x2+x-m=0没有实数根，则m≤0 |
| D、若m＞0，则关于x的方程x2+x-m=0没有实数根 |
在△ABC中，若a=2，c=4，B=60°，则b等于（ ）
A、2
| ||
| B、12 | ||
C、2
| ||
| D、28 |
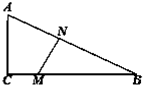有一块实验题，形如图的直角△ABC，其中∠C=90°，AC=50米，BC=120米，拟在边BC和BA之间开出一条水渠，即图示中线段MN，并且使这条水渠恰好能平分该实验题的面积．为节省人力、物力，要使这条水渠最短．问：应如何设计？水渠最短的长度为多少米？