题目内容
一个几何体的三视图如图所示，则这个几何体的表面积为（ ）
A、7+
| ||
B、9+
| ||
C、7+
| ||
D、9+
|
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中的三视图可得该几何体为，以俯视图为底面的四棱柱，底面是上底长1，下底长3，高为1的梯形，棱柱的高为1，求出底面积和侧面积后相加可得答案．
解答：
解：由已知中的三视图可得该几何体为，以俯视图为底面的四棱柱，底面是上底长1，下底长3，高为1的梯形，棱柱的高为1，
故底面面积为S底=
×(1+3)×1=2，
底面周长C=1+1+3+
=5+
，
故棱柱的侧面积S侧=（5+
）×1=5+
．
故这个几何体的表面积S=2×S底+S侧=9+
．
故选：B
故底面面积为S底=
| 1 |
| 2 |
底面周长C=1+1+3+
| 12+(3-1)2 |
| 5 |
故棱柱的侧面积S侧=（5+
| 5 |
| 5 |
故这个几何体的表面积S=2×S底+S侧=9+
| 5 |
故选：B
点评：本题考查的知识点为：由三视图求表面积，其中根据已知分析出几何体的形状是解答的关键．
练习册系列答案
相关题目
当α为第二象限角时，
-
的值是（ ）
| |sinα| |
| sinα |
| cosα |
| |cosα| |
| A、1 | B、0 | C、2 | D、-2 |
在集合{1，2，3，4}中任取一个偶数a和一个奇数b构成以原点为起点的向量
=（a，b）．从所有得到的以原点为起点的向量中任取两个向量为邻边作三角形，事件“所得三角形的面积等于1”的概率为（ ）
| α |
A、
| ||
B、
| ||
C、
| ||
D、
|
大小为-
的角的终边落在（ ）
| 11π |
| 4 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知L1：x-3y+7=0，L2：x+2y+4=0，下列说法正确的是（ ）
A、L1到L2的角为
| ||
B、L1到L2的角为
| ||
C、L2到L1的角为
| ||
D、L1到L2的夹角为
|
在△ABC中，若a=2，c=4，B=60°，则b等于（ ）
A、2
| ||
| B、12 | ||
C、2
| ||
| D、28 |
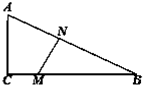有一块实验题，形如图的直角△ABC，其中∠C=90°，AC=50米，BC=120米，拟在边BC和BA之间开出一条水渠，即图示中线段MN，并且使这条水渠恰好能平分该实验题的面积．为节省人力、物力，要使这条水渠最短．问：应如何设计？水渠最短的长度为多少米？