题目内容
已知函数f(x)=
(a∈R且x≠a).
(1)证明:对定义域内所有x,f(x)+2+f(2a-x)恒为定值;
(2)设函数g(x)=x2+|(x-a)f(x)|,求g(x)的最小值.
| x+1-a |
| a-x |
(1)证明:对定义域内所有x,f(x)+2+f(2a-x)恒为定值;
(2)设函数g(x)=x2+|(x-a)f(x)|,求g(x)的最小值.
考点:函数恒成立问题,函数的最值及其几何意义
专题:函数的性质及应用
分析:(1)先根据已知得到f(2a-x),带入f(x)+2+f(2a-x)直接运算即可;
(2)分情况讨论x≥a-1和x<a-1两类情况,去掉绝对值,利用二次函数的性质,即可确定g(x)的最小值.
(2)分情况讨论x≥a-1和x<a-1两类情况,去掉绝对值,利用二次函数的性质,即可确定g(x)的最小值.
解答:
解(1)证明:∵f(x)=
,
∴f(2a-x)=
,
∴f(x)+2+f(2a-x)=
+2+
=
+2+
=
=0为定值
∴命题得证.
(2)g(x)=x2+|x+1-a|(x≠a)
①当x≥a-1且x≠a时,g(x)=x2+x+1-a=(x+
)2+
-a
如果a-1≥-
即a≥
时,则函数在[a-1,a)和(a,+∞)上单调递增g(x)min=g(a-1)=(a-1)2
如果a-1<-
即当a<
且a≠-
时,g(x)min=g(-
)=
-a
当a=-
时,g(x)最小值不存在;
②当x≤a-1时g(x)=x2-x-1+a=(x-
)2+a-
如果a-1>
即a>
时g(x)min=g(
)=a-
如果a-1≤
即a≤
时g(x)在(-∞,a-1)上为减函数g(x)min=g(a-1)=(a-1)2
当a>
时(a-1)2-(a-
)=(a-
)2>0,当a<
时(a-1)2-(
-a)=(a-
)2>0
综合得:当a<
且a≠-
时 g(x)最小值是
-a
当
≤a≤
时 g(x)最小值是(a-1)2;
当a>
时 g(x)最小值为a-
当a=-
时 g(x)最小值不存在.
| x+1-a |
| a-x |
∴f(2a-x)=
| 2a-x+1-a |
| a-2a+x |
∴f(x)+2+f(2a-x)=
| x+1-a |
| a-x |
| 2a-x+1-a |
| a-2a+x |
=
| x+1-a |
| a-x |
| a-x+1 |
| x-a |
| x+1-a+2a-2x-a+x-1 |
| a-x |
∴命题得证.
(2)g(x)=x2+|x+1-a|(x≠a)
①当x≥a-1且x≠a时,g(x)=x2+x+1-a=(x+
| 1 |
| 2 |
| 3 |
| 4 |
如果a-1≥-
| 1 |
| 2 |
| 1 |
| 2 |
如果a-1<-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
当a=-
| 1 |
| 2 |
②当x≤a-1时g(x)=x2-x-1+a=(x-
| 1 |
| 2 |
| 5 |
| 4 |
如果a-1>
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
如果a-1≤
| 1 |
| 2 |
| 3 |
| 2 |
当a>
| 3 |
| 2 |
| 5 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
综合得:当a<
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
当
| 1 |
| 2 |
| 3 |
| 2 |
当a>
| 3 |
| 2 |
| 5 |
| 4 |
当a=-
| 1 |
| 2 |
点评:本题考查绝对值函数的化简,利用二次函数性质求最值,以及分类讨论的数学思想,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知圆A:(x+2)2+y2=36,圆A内一定点B(2,0),圆P过B点且与圆A内切,则圆心P的轨迹为( )
| A、圆 | B、椭圆 |
| C、直线 | D、以上都不对 |
大小为-
的角的终边落在( )
| 11π |
| 4 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
在△ABC中,若a=2,c=4,B=60°,则b等于( )
A、2
| ||
| B、12 | ||
C、2
| ||
| D、28 |
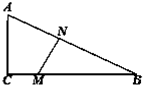 有一块实验题,形如图的直角△ABC,其中∠C=90°,AC=50米,BC=120米,拟在边BC和BA之间开出一条水渠,即图示中线段MN,并且使这条水渠恰好能平分该实验题的面积.为节省人力、物力,要使这条水渠最短.问:应如何设计?水渠最短的长度为多少米?
有一块实验题,形如图的直角△ABC,其中∠C=90°,AC=50米,BC=120米,拟在边BC和BA之间开出一条水渠,即图示中线段MN,并且使这条水渠恰好能平分该实验题的面积.为节省人力、物力,要使这条水渠最短.问:应如何设计?水渠最短的长度为多少米?