题目内容
（文）已知函数f（x）=x2+10x-a+3，当x∈[-2，+∞）时，f（x）≥0恒成立，求实数a的取值范围．
考点：二次函数的性质
专题：函数的性质及应用
分析：由条件利用二次函数的性质求得函数的最小值为f（-2）=-13-a，再由-13-a≥0，求得a的范围．
解答：
解：由于函数f（x）=x2+10x-a+3的图象的对称轴方程为x=-5，故函数在[-2，+∞）上单调递增，
故函数的最小值为f（-2）=-13-a．
由于当x∈[-2，+∞）时，f（x）≥0恒成立，
∴-13-a≥0，求得a≤-13．
故函数的最小值为f（-2）=-13-a．
由于当x∈[-2，+∞）时，f（x）≥0恒成立，
∴-13-a≥0，求得a≤-13．
点评：本题主要考查二次函数的性质，利用单调性求函数的最值，函数的恒成立问题，属于基础题．
练习册系列答案
相关题目
x2-x-6＜0的解集是（ ）
| A、（-∞，-2）∪（3，+∞） |
| B、（-2，3） |
| C、（2，3） |
| D、（-3，2） |
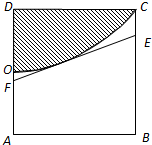如图，有一边长为2米的正方形钢板ABCD缺损一角（图中的阴影部分），边缘线OC是以直线AD为对称轴，以线段AD的中点O为顶点的抛物线的一部分．工人师傅要将缺损一角切割下来，使剩余的部分成为一个直角梯形．要得到函数y=sin（2x+
）的图象，只需将函数y=sin2x的图象（ ）
| π |
| 3 |
A、向左平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向右平移
|
已知A={x|x2-3x-10≤0}，B={x|x＞3}，则A∩B=（ ）
| A、{x|3＜x≤5} |
| B、{x|3≤x≤5} |
| C、{x|-2≤x≤3} |
| D、{x|x＞3} |