题目内容
14.已知向量$\overrightarrow a=(1,2)$,$\overrightarrow b=(x,6)$,且$\overrightarrow a$∥$\overrightarrow b$,则$|\overrightarrow a-\overrightarrow b|$=2$\sqrt{5}$.分析 利用向量共线定理、模的计算公式即可得出.
解答 解:∵$\overrightarrow a$∥$\overrightarrow b$,∴2x-6=0,解得x=3.
则$\overrightarrow{a}-\overrightarrow{b}$=(-2,-4),
则$|\overrightarrow a-\overrightarrow b|$=$\sqrt{(-2)^{2}+(-4)^{2}}$=2$\sqrt{5}$.
故答案为:$2\sqrt{5}$.
点评 本题考查了向量共线定理、模的计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
5.若集合M={x|log2x<1},集合N={x|x2-1≤0},则M∩N=( )
| A. | {x|1≤x<2} | B. | {x|-1≤x<2} | C. | {x|-1<x≤1} | D. | {x|0<x≤1} |
9.设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
| A. | “m∥α,m∥β”是“α∥β”的充分不必要条件 | |
| B. | m∥n时,“m∥β”是“n∥β”的必要不充分条件 | |
| C. | n?α时,“m⊥α”是“m⊥n”的既不充分也不必要条件 | |
| D. | m⊥α,n⊥β时,“m⊥n”是“α⊥β”的充要条件 |
6.设函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x<2}\\{{x}^{2},x≥2}\end{array}\right.$,若f(a+1)≥f(2a-1),则实数a的取值范围是( )
| A. | (-∞,1] | B. | (-∞,2] | C. | [2,6] | D. | [2,+∞) |
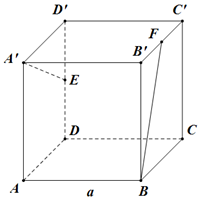 如图正方体ABCD-A′B′C′D′中,E、F为中点,
如图正方体ABCD-A′B′C′D′中,E、F为中点,