题目内容

19．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1，F2，点M与双曲线C的焦点不重合，点M关于F1，F2的对称点分别为A，B，线段MN的中点在双曲线的右支上，若|AN|-|BN|=12，则a=（　　）
A．3B．4C．5D．6

分析 根据已知条件，作出图形，MN的中点连接双曲线的两个焦点，便会得到三角形的中位线，根据中位线的性质及双曲线上的点到两焦点的距离之差的绝对值为2a，求出||AN|-|BN||，可得结论．

解答 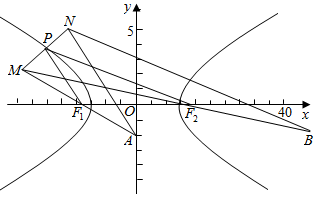解：设双曲线C的左右焦点分别为F1，F2，如图，
连接PF1，PF2，
∵F1是MA的中点，P是MN的中点，
∴F1P是△MAN的中位线，
∴|PF1|=$\frac{1}{2}$|AN|，
同理|PF2|=$\frac{1}{2}$|BN|，
∴||AN|-|BN||=2||PF1|-|PF2||，
∵P在双曲线上，
根据双曲线的定义知：||PF1|-|PF2||=2a，
∴||AN|-|BN||=4a=12，∴a=3．
故选A．

点评 本题考查双曲线的定义、方程和性质，同时考查三角形的中位线，运用定义法是解题的关键，属于中档题．

练习册系列答案
相关题目
9．设m，n是两条不同的直线，α，β是两个不同的平面，则下列命题正确的是（　　）
A．“m∥α，m∥β”是“α∥β”的充分不必要条件
B．m∥n时，“m∥β”是“n∥β”的必要不充分条件
C．n?α时，“m⊥α”是“m⊥n”的既不充分也不必要条件
D．m⊥α，n⊥β时，“m⊥n”是“α⊥β”的充要条件
10．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左、右焦点分别为F1，F2，离心率为$\frac{1}{2}$，在x轴上有一点M（-3，0）满足$\overrightarrow{M{F_2}}=2\overrightarrow{M{F_1}}$．
（1）求椭圆C的方程；
（2）直线l与直线x=2交于点A，与直线x=-2交于点B，且$\overrightarrow{{F_2}A}•\overrightarrow{{F_2}B}=0$，判断并证明直线l与椭圆C的交点个数．
7．已知函数f（x）=ln（x+1）-$\frac{{a{x^2}+x}}{{{{（{1+x}）}^2}}}$．
（1）当a=1时，求函数f（x）在x=e-1处的切线方程；
（2）当$\frac{2}{3}$＜a≤2时，讨论函数f（x）的单调性；
（3）若x＞0，求函数g（x）=（1+$\frac{1}{x}}$）x（1+x）${\;}^{\frac{1}{x}}}$的最大值．
14．命题p：“?x∈N+，（$\frac{1}{2}$）x≤$\frac{1}{2}$”的否定为（　　）
A．?x∈N+，（$\frac{1}{2}$）x＞$\frac{1}{2}$B．?x∉N+，（$\frac{1}{2}$）x＞$\frac{1}{2}$C．?x∉N+，（$\frac{1}{2}$）x＞$\frac{1}{2}$D．?x∈N+，（$\frac{1}{2}$）x＞$\frac{1}{2}$
4．已知数列{an}是公差不为0的等差数列，首项a1=1，且a1，a2，a4成等比数列．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设数列{bn}满足bn=an+2${\;}^{{a}_{n}}$，求数列{bn}的前n项和Tn．
11．已知平面向量$\overrightarrow{a}$=（k，3），$\overrightarrow{b}$=（1，4），若$\overrightarrow{a}$⊥$\overrightarrow{b}$，则实数k为（　　）
A．-12B．12C．$\frac{4}{3}$D．$\frac{3}{4}$
8．已知椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$，则以点$（2，\frac{3}{2}）$为中点的弦所在的直线方程为（　　）
A．8x-6y-7=0B．3x+4y=0C．3x+4y-12=0D．6x+8y-25=0
15．若-$\frac{π}{8}$＜θ＜0，则sinθ，cosθ，tanθ的大小关系为（　　）
A．sinθ＜tanθ＜cosθB．tanθ＜sinθ＜cosθC．tanθ＜cosθ＜sinθD．sinθ＜cosθ＜tanθ

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网