题目内容
1.如图,点O为△ABC的重心,OA⊥OB,且AB=2,则$\overrightarrow{AC}$•$\overrightarrow{BC}$的值为8.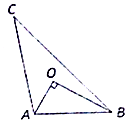
分析 取三角形三边中点,用三边向量表示出$\overrightarrow{AO},\overrightarrow{BO}$,根据向量垂直列方程化简即可得出答案.
解答  解:延长AO交BC于D,延长CO交AB于E,延长BO交AC于F
解:延长AO交BC于D,延长CO交AB于E,延长BO交AC于F
∵O是△ABC的重心,∴D,E,F分别是BC,AB,AC的中点,
∴$\overrightarrow{AO}=\frac{2}{3}\overrightarrow{AD}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC})$,
$\overrightarrow{BO}=\frac{2}{3}\overrightarrow{BF}$=$\frac{1}{3}$($\overrightarrow{BA}+\overrightarrow{BC}$),
∵OA⊥OB,∴$\overrightarrow{AO}•\overrightarrow{BO}=0$,即($\overrightarrow{AB}+\overrightarrow{AC}$)•($\overrightarrow{BA}+\overrightarrow{BC}$)=0,
∴-${\overrightarrow{AB}}^{2}$+$\overrightarrow{AB}•\overrightarrow{BC}$+$\overrightarrow{AC}•\overrightarrow{BA}$+$\overrightarrow{AC}•\overrightarrow{BC}$=0,
∴-${\overrightarrow{AB}}^{2}$+$\overrightarrow{AB}$•($\overrightarrow{BC}-\overrightarrow{AC}$)+$\overrightarrow{AC}•\overrightarrow{BC}$=0,
∴-2${\overrightarrow{AB}}^{2}$+$\overrightarrow{AC}•\overrightarrow{BC}$=0,
∴$\overrightarrow{AC}•\overrightarrow{BC}$=2${\overrightarrow{AB}}^{2}$=8.
故答案为:8.
点评 本题考查了平面向量的基本定理,平面向量的数量积运算,属于中档题.

| A. | (1,1,1) | B. | (1,2,2) | C. | (1,2,4) | D. | (1,1,2) |
| A. | (-$\frac{1}{3}$,+∞) | B. | ($\frac{1}{3}$,1) | C. | (-∞,-$\frac{1}{3}$) | D. | (-1,-$\frac{1}{3}$) |
| A. | $\frac{{3\sqrt{5}}}{2}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{2}$ | D. | $\frac{3}{2}$ |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
(1)根据以上数据建立一个2×2的列联表;
(2)判断是否能有95%的把握说晕机与性别有关?
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |