Question

4．一线性规划问题的可行域为坐标平面上的正八边形ABCDEFGH及其内部（如图），已知目标函数z=3+ax+by（a，b∈R）的最大值只在顶点B处，如果目标函数变成z=3-bx-ay时，最大值只在顶点（　　）

• A． A
• B． B
• C． C
• D． D

Answer 1

分析 目标函数z=3+ax+by（a，b∈R）可化为：y=$-\frac{a}{b}x-\frac{3}{b}+\frac{z}{b}$由目标函数z=3+ax+by（a，b∈R）的最大值只在顶点B处，得  $-\frac{a}{b}＞{k}_{AB}=\sqrt{3}$，且b＜0，a＞0．从而得到目标函数变成z=3-bx-ay的最大值只在顶点A处，

解答 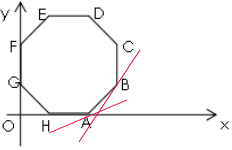解：目标函数z=3+ax+by（a，b∈R）可化为：y=$-\frac{a}{b}x-\frac{3}{b}+\frac{z}{b}$
∵目标函数z=3+ax+by（a，b∈R）的最大值只在顶点B处，
∴$-\frac{a}{b}＞{k}_{AB}=\sqrt{3}$，且b＜0，a＞0．
目标函数变成z=3-bx-ay可化为y=$-\frac{b}{a}x+\frac{3}{a}-\frac{z}{a}$，
∵$-\frac{b}{a}∈（0，\frac{\sqrt{3}}{3}），\frac{1}{a}＜0$，∴目标函数变成z=3-bx-ay时，最大值只在顶点A处，
故选：A

点评 本题考查了线性规划问题，依据直线斜率、纵截距、最优解的范围，确定参数a、b的取值是解题关键，属于中档题