题目内容
20.若某多面体的三视图如图所示(单位:cm),则此多面体的体积是$\frac{5}{6}$cm3.
分析 根据三视图得该几何体是由棱长为1cm的正方体、沿相邻三个侧面的对角线截去一个三棱锥得到一个多面体,画出图,由正方体的体积和椎体的体积公式求出此多面体的体积即可.
解答 解:根据三视图得该几何体是由棱长为1cm的正方体ABCD-EFGH、
如图所示: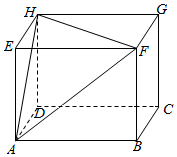 ,
,
沿相邻三个侧面的对角线截去一个三棱锥E-AFH得到一个多面体,
此多面体的体积V=1-$\frac{1}{3}$×$\frac{1}{2}$×1×1×1=$\frac{5}{6}$(cm3);
故答案为:$\frac{5}{6}$.
点评 本题考查三视图求几何体的体积、由三视图正确复原几何体是解题的关键,考查空间想象能力.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
6.已知函数$f(x)=\left\{\begin{array}{l}-{x^2}+4x,x≤2\\{log_2}x-a,x>2\end{array}\right.$有两个不同的零点,则实数a的取值范围是( )
| A. | [-1,0) | B. | (1,2] | C. | (1,+∞) | D. | (2,+∞) |
11.以长方形ABCD-A1B1C1D1的棱AB,AD,AA1所在的直线为坐标轴建立空间直角坐标系,且长方体的棱AB=1,AD=2,AA1=4,则棱CC1中点坐标为( )
| A. | (1,1,1) | B. | (1,2,2) | C. | (1,2,4) | D. | (1,1,2) |
8.函数$f(x)=tan(2x-\frac{π}{6})$的最小正周期是( )
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
12.已知函数f(x)=|x+3|+2,g(x)=kx+1,若方程f(x)=g(x)有两个不相等的实根,则实数a的取值范围是( )
| A. | (-$\frac{1}{3}$,+∞) | B. | ($\frac{1}{3}$,1) | C. | (-∞,-$\frac{1}{3}$) | D. | (-1,-$\frac{1}{3}$) |
9.过抛物线y2=4x的焦点F的直线与其交于A,B两点,|AF|>|BF|,如果|AF|=5,那么|BF|=( )
| A. | $\frac{{3\sqrt{5}}}{2}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{2}$ | D. | $\frac{3}{2}$ |
10.复数z满足z=(5+2i)2,则z的共轭复数在复平面上对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |