Question

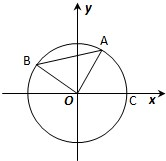如图，A，B是单位圆O上的动点，且A，B分别在第一，二象限．C是圆与x轴的交点，△AOB为正三角形．若A点的坐标为（x，y）．记∠COA=α，求|BC|²的取值范围．

Answer 1

考点：三角函数线

专题：三角函数的图像与性质

分析：A的坐标为（coaα，sinα），根据三角函数的定义可知，sinα和cosα的值，cos∠COB=cos（α+60°），利用两角和的余弦公式展开运算，利用余弦定理求|BC|²的取值范围．

解答： 解：∵A的坐标为（x，y），根据三角函数的定义可知，y=sinα，x=cosα，
即A（coaα，sinα），
∵△AOB为正三角形，∴∠AOB=60°．
∴cos∠COB=cos（α+60°）=cosαcos60°-sinαsin60°=

1

2

cosα-

3

2

sinα，
∴|BC|² =|OC|²+|OB|²-2|OC|•|OB|cos∠COB=1+1-2×（

1

2

cosα-

3

2

sinα）=2-cosα+

3

sinα=2+2sin（α-30°），
∵A，B分别在第一，二象限．
∴

0°＜α＜90° 90°＜α+60°＜180°

即30°＜α＜90°，
∴0°＜α-30°＜60°，
∴0＜sin（α-30°）＜

3

2

，
即0＜2sin（α-30°）＜

3

，
∴2＜2+2sin（α-30°）＜2+

3

，
即|BC|²的取值范围是（2，2+

3

）．

点评：本题考查任意角的三角函数的定义，两角和的余弦公式的应用，余弦定理的应用，考查计算能力．圆．综合性较强，要求熟练掌握两角和差的公式以及辅助角公式的应用．