题目内容
设a为常数,求点A(0,a)与椭圆
+
=1上一点P(x,y)所连线段长的最大值.
| x2 |
| 25 |
| y2 |
| 9 |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:先表示出f(x)=AP2=-
-2ay+a2+25,确定对称轴,利用分类讨论,即可得出结论.
| 16y2 |
| 9 |
解答:
解:AP2=x2+(y-a)2,又x2=25-
,
∴f(x)=AP2=-
-2ay+a2+25
对称轴y=-
,-3≤y≤3,
-
<-3时,a>
,f(x)max=f(-3)=a2+6a+9,∴APmax=a+3;
-3≤-
≤3时,-
≤a≤
,f(x)max=f(-
)=
+25,∴APmax=
;
-
>3时,a<-
,f(x)max=f(3)=a2-6a+9=3-a.
| 25y2 |
| 9 |
∴f(x)=AP2=-
| 16y2 |
| 9 |
对称轴y=-
| 9a |
| 16 |
-
| 9a |
| 16 |
| 16 |
| 3 |
-3≤-
| 9a |
| 16 |
| 16 |
| 3 |
| 16 |
| 3 |
| 9a |
| 16 |
| 25a2 |
| 16 |
| 5 |
| 4 |
| a2+16 |
-
| 9a |
| 16 |
| 16 |
| 3 |
点评:本题考查直线与椭圆的综合,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 某广告公司设计一个凸八边形的商标,它的中间是一个正方形,外面是四个腰长为1,顶角为2α的等腰三角形.
某广告公司设计一个凸八边形的商标,它的中间是一个正方形,外面是四个腰长为1,顶角为2α的等腰三角形.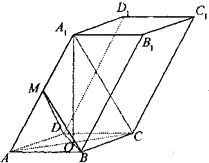 已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形,AC∩BD=O,AA1=2
已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形,AC∩BD=O,AA1=2