题目内容
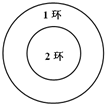 如图,一半径为
如图,一半径为| 3 |
(Ⅰ)求该同学在一次投掷中获得2环的概率;
(Ⅱ)设X表示该同学在3次投掷中获得的环数,求X的分布列及数学期望.
考点:离散型随机变量的期望与方差,几何概型
专题:计算题,概率与统计
分析:(1)题考查的知识点是几何概型的意义,关键是要找出满足条件A的区域面积和总面积之间的关系,再根据几何概型计算公式给出答案;
(2)根据(1)中投中A区域的概率,不难列出x的分布列并进行数学期望.
(2)根据(1)中投中A区域的概率,不难列出x的分布列并进行数学期望.
解答:
 解:(I)设该同学在一次投掷中投中2环的概率为P(A),
解:(I)设该同学在一次投掷中投中2环的概率为P(A),
由题意可得是几何概型,P(A)=
=
=
∴该同学一次投掷投中2环的概率为
.
(II)由题意可知X可能的值为3,4,5,6,
P(X=3)=(1-
)3,P(X=4)
(
)(1-
)2=
,P(X=5)
(
)2(1-
) =
,P(X=6)=
(
)3=
∴X的分布列为
∴E(X)=3×
+4×
+5×
+6×
=4环
答:X的数学期望为4环.
 解:(I)设该同学在一次投掷中投中2环的概率为P(A),
解:(I)设该同学在一次投掷中投中2环的概率为P(A),由题意可得是几何概型,P(A)=
| S内 |
| S大 |
| π×12 | ||
π×
|
| 1 |
| 3 |
∴该同学一次投掷投中2环的概率为
| 1 |
| 3 |
(II)由题意可知X可能的值为3,4,5,6,
P(X=3)=(1-
| 1 |
| 3 |
| =C | 1 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 9 |
| =C | 2 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 9 |
| C | 3 3 |
| 1 |
| 3 |
| 1 |
| 27 |
∴X的分布列为
| X | 3 | 4 | 5 | 6 | ||||||||
| P |
|
|
|
|
| 8 |
| 27 |
| 4 |
| 9 |
| 2 |
| 9 |
| 1 |
| 27 |
答:X的数学期望为4环.
点评:求古典概型的概率的基本步骤为:(1)算出所有基本事件的个数n.(2)求出事件A包含的所有基本事件数m.(3)代入公式,求出P(A).几何概型中的三种基本度量为长度、面积和体积,在解题时要准确把握,要把问题向它们作合理地转化,要注意古典概型与几何概型的区别(基本事件的有限性和无限性),正确选用几何概型解题.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
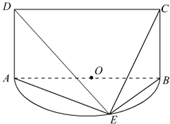 如图,E是以AB为直径的半圆O上异于A、B的点,矩形ABCD所在的平面垂直于半圆O所在的平面,且AB=2AD=2a.
如图,E是以AB为直径的半圆O上异于A、B的点,矩形ABCD所在的平面垂直于半圆O所在的平面,且AB=2AD=2a.