题目内容
已知函数f(x)=x2-2ax-3在x∈[2,4]上最大值为5,求a的值.
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:由题意得,函数f(x)的对称轴为:x=a,再分对称轴在区间的左侧、右侧、中间三种情况,分别根据函数在区间[2,4]上有最大值5,求出实数a的值.
解答:
解:由f(x)=(x-a)2-a2-3,得函数f(x)的对称轴为:x=a,
①当a>4时,f(x)在[2,4]上递减,根据函数在区间[2,4]上有最大值5,可得f(2)=5,即a=-1,与a>4矛盾;
②当a<2时,f(x)在[2,4]上递增,根据函数在区间[2,4]上有最大值5,可得f(4)=5,解得a=1.
③当2≤a≤4时,f(x)在[2,a]递增,在[a,4]上递减,根据函数在[2,4]上有最大值5,可得f(a)=5,即-a2=8,无解.
综上,a=1.
①当a>4时,f(x)在[2,4]上递减,根据函数在区间[2,4]上有最大值5,可得f(2)=5,即a=-1,与a>4矛盾;
②当a<2时,f(x)在[2,4]上递增,根据函数在区间[2,4]上有最大值5,可得f(4)=5,解得a=1.
③当2≤a≤4时,f(x)在[2,a]递增,在[a,4]上递减,根据函数在[2,4]上有最大值5,可得f(a)=5,即-a2=8,无解.
综上,a=1.
点评:本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,体现了分类讨论的数学思想.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
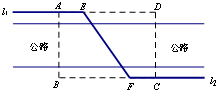 如图,某自来水公司要在公路两侧铺设水管,公路为东西方向,在路北侧沿直线铺设线路l1,在路南侧沿直线铺设线路l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=80m,公路两侧铺设水管的费用为每米1万元,穿过公路的EF部分铺设水管的费用为每米2万元,设∠EFB=
如图,某自来水公司要在公路两侧铺设水管,公路为东西方向,在路北侧沿直线铺设线路l1,在路南侧沿直线铺设线路l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=80m,公路两侧铺设水管的费用为每米1万元,穿过公路的EF部分铺设水管的费用为每米2万元,设∠EFB=