题目内容
12.己知函数f(x)=2cos(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的最小正周期为π,直线x=-$\frac{π}{24}$为它的图象的一条对称轴.(1)求ω,φ的值;
(2)在△ABC中a,b,c分别为角A,B,C的对应边,若f(-$\frac{A}{2}$)=$\sqrt{2}$,a=3,b+c=6,求b,c值.
分析 (1)由已知利用三角函数周期公式可求ω,由余弦函数的对称性,结合范围0<φ<$\frac{π}{2}$可求φ的值.
(2)由已知可求$cos(A-\frac{π}{12})=\frac{{\sqrt{2}}}{2}$,结合范围-$\frac{π}{12}$<A-$\frac{π}{12}$<$\frac{11π}{12}$,可求A的值,进而利用余弦定理可求bc=9,结合a+c=6,即可得解b,c的值.
解答 (本题满分10分)
解:(1)函数f(x)的最小正周期为π=$\frac{2π}{ω}$,∴ω=2,…(2分)
x=-$\frac{π}{24}$为f(x)的图象的一条对称轴,
∴$2×(-\frac{π}{24})+ϕ=kπ(0<ϕ<\frac{π}{2})∴ϕ=\frac{π}{12}$…(5分)
(2)∵$f(-\frac{A}{2})=2cos(A-\frac{π}{12})=\sqrt{2}$,
∴$cos(A-\frac{π}{12})=\frac{{\sqrt{2}}}{2}$,
∵-$\frac{π}{12}$<A-$\frac{π}{12}$<$\frac{11π}{12}$,
∴A-$\frac{π}{12}$=$\frac{π}{4}$,解得:A=$\frac{π}{3}$,…(7分)
∵a2=b2+c2-2bccosA=(b+c)2-3bc,即bc=9. …(9分)
又∵b+c=6,
∴解得到b=c=3.…(10分)
点评 本题主要考查了三角函数周期公式,余弦函数的对称性,余弦定理在解三角形中的应用,考查了数形结合思想和转化思想,属于中档题.

练习册系列答案
相关题目
20.直线 y+3=0的倾斜角是( )
| A. | 0° | B. | 45° | C. | 90° | D. | 不存在 |
7.9-2=( )
| A. | 81 | B. | $\frac{1}{81}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{9}$ |
4.已知m=$\frac{tan(α+β+γ)}{tan(α-β+γ)}$,若sin2(α+γ)=3sin2β,则m=( )
| A. | -1 | B. | $\frac{3}{4}$ | C. | $\frac{3}{2}$ | D. | 2 |
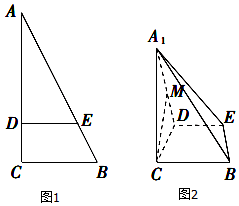 如图,在△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2.将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD.
如图,在△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2.将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD. 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,$\sqrt{2}$),离心率e=$\frac{\sqrt{2}}{2}$,直线l的渐近线为x=4.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,$\sqrt{2}$),离心率e=$\frac{\sqrt{2}}{2}$,直线l的渐近线为x=4.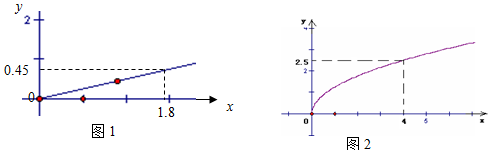
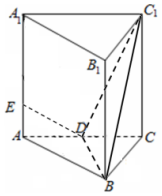 已知正三棱柱ABC-A1B1C1中,AB=AA1=2,点D为AC的中点,点E为AA1上.
已知正三棱柱ABC-A1B1C1中,AB=AA1=2,点D为AC的中点,点E为AA1上.