题目内容
2.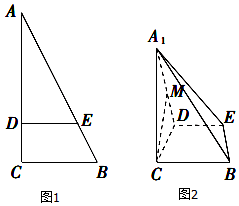 如图,在△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2.将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD.
如图,在△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2.将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD.(1)若M是A1D的中点,求A1B与平面CME所成角的正弦值;
(2)线段A1B上是否存在点P,使平面PME与平面CME垂直,若存在,求$\frac{{{A_1}P}}{{{A_1}B}}$的值,若不存在,请说明理由.
分析 (1)建立如图所示的坐标系,求出平面CME的法向量,利用向量方法求A1B与平面CME所成角的正弦值;
(2)求出平面PME的法向量,由$\overrightarrow{m}•\overrightarrow{n}$=0,可得结论.
解答 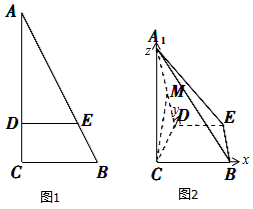 解:(1)建立如图所示的坐标系,则C(0,0,0),M(0,1,$\sqrt{3}$),E(2,2,0),A1(0,0,2$\sqrt{3}$),B(3,0,0),
解:(1)建立如图所示的坐标系,则C(0,0,0),M(0,1,$\sqrt{3}$),E(2,2,0),A1(0,0,2$\sqrt{3}$),B(3,0,0),
∴$\overrightarrow{{A}_{1}B}$=(3,0,-2$\sqrt{3}$),$\overrightarrow{CM}$=(0,1,$\sqrt{3}$),$\overrightarrow{CE}$=(2,2,0),
设平面CME的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{y+\sqrt{3}z=0}\\{2x+2y=0}\end{array}\right.$,取$\overrightarrow{n}$=(3,-3,$\sqrt{3}$),
∴A1B与平面CME所成角的正弦值=|$\frac{9-6}{\sqrt{9+12}•\sqrt{9+9+3}}$|=$\frac{1}{7}$;
(2)设$\overrightarrow{{A}_{1}P}$=λ$\overrightarrow{{A}_{1}B}$,则P(3λ,0,2$\sqrt{3}$-2$\sqrt{3}$λ),$\overrightarrow{PM}$=(-3λ,1,-$\sqrt{3}$+2$\sqrt{3}$λ),$\overrightarrow{ME}$=(2,1,-$\sqrt{3}$)
设平面PME的法向量为$\overrightarrow{m}$=(a,b,c),则$\left\{\begin{array}{l}{-3λa+b+(-\sqrt{3}+2\sqrt{3}λ)c=0}\\{2a+b-\sqrt{3}c=0}\end{array}\right.$,取$\overrightarrow{m}$=(2$\sqrt{3}$λ,2$\sqrt{3}$-$\sqrt{3}$λ,2+3λ),
由$\overrightarrow{m}•\overrightarrow{n}$=0,可得λ=$\frac{1}{4}$,
∴$\frac{{{A_1}P}}{{{A_1}B}}$=$\frac{1}{4}$.
点评 本题考查线面角,考查平面与平面垂直的运用,考查向量方法,考查学生分析解决问题的能力,属于中档题.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案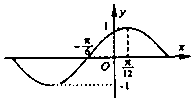
| A. | $y=sin({x+\frac{π}{6}})$ | B. | $y=cos({2x-\frac{π}{6}})$ | C. | $y=sin({2x-\frac{π}{6}})$ | D. | $y=cos({4x-\frac{π}{3}})$ |
| A. | -x2-2sinx | B. | -x2+2sinx | C. | x2+2sinx | D. | x2-2sinx |
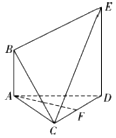 如图所示的多面体ABCDE中,已知AB∥DE,AB⊥AD,AD=2$\sqrt{3}$,AC=CD=DE=2AB=2,BC=$\sqrt{5}$,F是CD的中点.
如图所示的多面体ABCDE中,已知AB∥DE,AB⊥AD,AD=2$\sqrt{3}$,AC=CD=DE=2AB=2,BC=$\sqrt{5}$,F是CD的中点. 如图,已知斜三棱柱ABC-A1B1C1的所有棱长均为2,∠B1BA=$\frac{π}{3}$,M,N分别为A1C1与B1C的中点,且侧面ABB1A1⊥底面ABC.
如图,已知斜三棱柱ABC-A1B1C1的所有棱长均为2,∠B1BA=$\frac{π}{3}$,M,N分别为A1C1与B1C的中点,且侧面ABB1A1⊥底面ABC.