题目内容
1.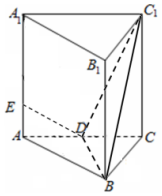 已知正三棱柱ABC-A1B1C1中,AB=AA1=2,点D为AC的中点,点E为AA1上.
已知正三棱柱ABC-A1B1C1中,AB=AA1=2,点D为AC的中点,点E为AA1上.(Ⅰ)当AA1=4AE时,求证:DE⊥平面BDC1;
(Ⅱ)当AA1=2AE时,求三棱锥C1-EBD的体积.
分析 (Ⅰ)证明BD⊥AC,BD⊥DE.连接EC1,证明ED⊥C1D,然后证明DE⊥平面BDC1.
(Ⅱ)求出${S_{△{C_1}DE}}=\frac{3}{2}$,说明BD为三棱锥B-C1DE的高,然后利用等体积法转化求解即可.
解答 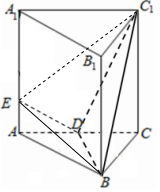 (Ⅰ)证明:∵△ABC为正三角形,点D为AC的中点,
(Ⅰ)证明:∵△ABC为正三角形,点D为AC的中点,
∴BD⊥AC,∴BD⊥面ACC1A1,从而BD⊥DE.
连接EC1,∵AA1=4AE,AB=AA1=2,∴$EA=\frac{1}{2}$,$ED=\frac{{\sqrt{5}}}{2}$,$E{C_1}=\sqrt{{2^2}+\frac{9}{4}}=\frac{5}{2}$,${C_1}D=\sqrt{5}$,
则$EC_1^2=E{D^2}+{C_1}{D^2}$,∴ED⊥C1D,
又C1D∩BD=D,∴DE⊥平面BDC1.
(Ⅱ)解:∵AA1=2AE,∴$ED=\sqrt{2},{C_1}D={C_1}E=\sqrt{5}$,∴${S_{△{C_1}DE}}=\frac{3}{2}$,
由(Ⅰ)知BD⊥面ACC1A1中,所以BD为三棱锥B-C1DE的高,
所以${V_{{C_1}-EBD}}={V_{B-{C_1}DE}}=\frac{1}{3}{S_{△{C_1}DE}}•BD=\frac{1}{3}×\frac{3}{2}×\sqrt{3}=\frac{{\sqrt{3}}}{2}$.
点评 本题考查直线与平面垂直的判定定理的应用,几何体的体积的求法,等体积法的应用,考查空间想象能力以及计算能力.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
16.执行如图所示的程序框图,当a=2,b=3时,输出s值为( )


| A. | 6 | B. | 8 | C. | 24 | D. | 36 |
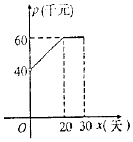 根据市场调查,某种新产品投放市场的30天内,每件的销售价格p(千元)与时间x(天)组成有序数对(x,p),点(x,p)落在下图中的两条线段上,且日销售量q(件)与时间x(天)之间的关系是q=-x+60(x∈N*).
根据市场调查,某种新产品投放市场的30天内,每件的销售价格p(千元)与时间x(天)组成有序数对(x,p),点(x,p)落在下图中的两条线段上,且日销售量q(件)与时间x(天)之间的关系是q=-x+60(x∈N*).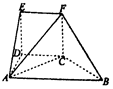 如图,几何体EF-ABCD中,DE⊥平面ABCD,CDEF是正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,△ACB的腰长为$2\sqrt{2}$的等腰直角三角形.
如图,几何体EF-ABCD中,DE⊥平面ABCD,CDEF是正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,△ACB的腰长为$2\sqrt{2}$的等腰直角三角形.