题目内容
4.已知m=$\frac{tan(α+β+γ)}{tan(α-β+γ)}$,若sin2(α+γ)=3sin2β,则m=( )| A. | -1 | B. | $\frac{3}{4}$ | C. | $\frac{3}{2}$ | D. | 2 |
分析 利用两角而和差的三角公式化简所给的式子,求得m的值.
解答 解:∵sin2(α+γ)=3sin2β,∴sin[(α+γ+β)-(β-α-γ)]=3sin[(α+γ+β)-(α+γ-β)],
∴sin(α+γ+β)cos(β-α-γ)-cos(α+γ+β)sin(β-α-γ)=3sin(α+γ+β)cos(α+γ-β)-3 cos(α+γ+β)sin(β-α-γ),
∴sin(α+γ+β)cos(α+γ-β)+cos(α+β+γ)sin(α+γ-β)=3sin(α+γ+β)cos(α+γ-β)+3cos(α+γ+β)sin(α+γ-β),
∴-2sin(α+γ+β)cos(α+γ-β)=2cos(α+γ+β)sin(α+γ-β),
∴-tan(α+γ+β)=tan(α+γ-β),
故m=$\frac{tan(α+β+γ)}{tan(α-β+γ)}$=-1,
故选:A.
点评 本题主要考查两角而和差的三角公式的应用,属于基础题.

练习册系列答案
相关题目
19.已知函数f(x)=$\left\{\begin{array}{l}(3a-2)x+6a-1(x<1)\\{a^x}(x≥1)\end{array}\right.$单调递减,那么实数a的取值范围是( )
| A. | (0,1) | B. | (0,$\frac{2}{3}$) | C. | [$\frac{3}{8}$,$\frac{2}{3}$) | D. | [$\frac{3}{8}$,1) |
16.执行如图所示的程序框图,当a=2,b=3时,输出s值为( )


| A. | 6 | B. | 8 | C. | 24 | D. | 36 |
 如图,已知斜三棱柱ABC-A1B1C1的所有棱长均为2,∠B1BA=$\frac{π}{3}$,M,N分别为A1C1与B1C的中点,且侧面ABB1A1⊥底面ABC.
如图,已知斜三棱柱ABC-A1B1C1的所有棱长均为2,∠B1BA=$\frac{π}{3}$,M,N分别为A1C1与B1C的中点,且侧面ABB1A1⊥底面ABC.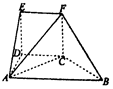 如图,几何体EF-ABCD中,DE⊥平面ABCD,CDEF是正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,△ACB的腰长为$2\sqrt{2}$的等腰直角三角形.
如图,几何体EF-ABCD中,DE⊥平面ABCD,CDEF是正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,△ACB的腰长为$2\sqrt{2}$的等腰直角三角形. 如图,已知平行四边形ABCD的三个顶点的坐标为A(-1,4),B(-2,-1),C(2,3).
如图,已知平行四边形ABCD的三个顶点的坐标为A(-1,4),B(-2,-1),C(2,3).