题目内容
20.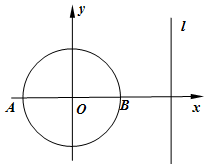 如图,在平面直角坐标系中,已知圆O:x2+y2=4与直线l:x=4,A,B是圆O与x轴的交点,P是l上的动点.
如图,在平面直角坐标系中,已知圆O:x2+y2=4与直线l:x=4,A,B是圆O与x轴的交点,P是l上的动点.(1)若从P到圆O的切线长为$2\sqrt{3}$,求点P的坐标;
(2)若直线PA,PB与圆O的另一个交点分别为M,N,求证:直线MN经过定点.
分析 (1)设点P的坐标为(4,a),设PD是圆O的切线,D是切点,则OD⊥PD.然后利用勾股定理列式求得a,则P的坐标可求;
(2)由题意知:A(-2,0),B(2,0),设P(4,a),求出直线PA方程,与圆的方程联立求得M坐标,同理求得N的坐标,然后分MN⊥x轴和MN与x轴不垂直分类求出MN所在直线方程,可得直线MN经过定点.
解答 (1)解:设点P的坐标为(4,a),设PD是圆O的切线,D是切点,则OD⊥PD.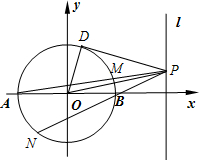
在Rt△PDO中,PO2=PD2+OD2=12+4=16,
即16+a2=16,∴a=0,
故点P的坐标为(4,0);
(2)证明:由题意知:A(-2,0),B(2,0),设P(4,a),直线PA方程为:$y=\frac{a}{6}(x+2)$,
由$\left\{\begin{array}{l}{x^2}+{y^2}=4\\ y=\frac{a}{6}(x+2)\end{array}\right.$,得(a2+36)x2+4a2x+4(a2-36)=0,
解得x=-2,$x=-\frac{{2({a^2}-36)}}{{{a^2}+36}}$,∴$M(-\frac{{2({a^2}-36)}}{{{a^2}+36}},\frac{24a}{{{a^2}+36}})$,
同理可求$N(\frac{{2({a^2}-4)}}{{{a^2}+4}},\frac{-8a}{{{a^2}+4}})$.
①若MN⊥x轴,则$-\frac{{2({a^2}-36)}}{{{a^2}+36}}=\frac{{2({a^2}-4)}}{{{a^2}+4}}$,
解得a2=12,此时点M,N的横坐标都为1,直线MN过定点(1,0);
②若MN与x轴不垂直,即a2≠12,此时${k_{MN}}=\frac{{\frac{-8a}{{{a^2}+4}}-\frac{24a}{{{a^2}+36}}}}{{\frac{{2({a^2}-4)}}{{{a^2}+4}}+\frac{{2({a^2}-36)}}{{{a^2}+36}}}}=\frac{-8a}{{{a^2}-12}}$,
∴直线MN的方程为:$y-\frac{-8a}{{{a^2}+4}}=\frac{-8a}{{{a^2}-12}}(x-\frac{{2({a^2}-4)}}{{{a^2}+4}})$,
即$y=\frac{-8a}{{{a^2}-12}}(x-1)$,直线MN过定点(1,0).
综上,直线MN过定点(1,0).
点评 本题考查直线与圆位置关系的应用,考查直线恒过定点问题,体现了分类讨论的数学思想方法,是中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $({0,\frac{1}{2}})∪({1,+∞})$ | B. | $({-∞,\frac{1}{2}})∪({1,+∞})$ | C. | (0,1) | D. | $({0,\frac{1}{2}})$ |
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{1}{4}$ |
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $2\sqrt{2}$ |
| A. | -ln2 | B. | ln2 | C. | 2$\sqrt{e}$-3 | D. | e2-3 |