题目内容
6.若$tan({α+\frac{π}{4}})=-3$,则cos2α+2sin2α=( )| A. | $\frac{9}{5}$ | B. | 1 | C. | $-\frac{3}{5}$ | D. | 0 |
分析 原式利用同角三角函数间的基本关系变形,将tanα的值代入计算即可求出值.
解答 解:由$tan({α+\frac{π}{4}})=-3$,得
$\frac{tanα+1}{1-tanα}$=-3,
解得tanα=2,
所以cos2α+2sin2α=$\frac{co{s}^{2}α+4sinαcosα}{co{s}^{2}α+si{n}^{2}α}$=$\frac{1+4tanα}{1+ta{n}^{2}α}$=$\frac{1+4×2}{1+{2}^{2}}$=$\frac{9}{5}$.
故选A.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
16.已知f(x)是定义在区间(0,+∞)上的函数,其导函数为f'(x),且不等式xf'(x)<2f(x)恒成立,则( )
| A. | 4f(1)<f(2) | B. | 4f(1)>f(2) | C. | f(1)<4f(2) | D. | f(1)<2f'(2) |
17.如图为某几何体的三视图,则该几何体的外接球的表面积为( )
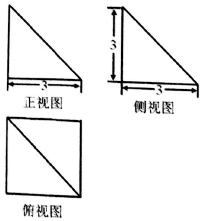

| A. | $\frac{27}{2}π$ | B. | 27π | C. | 27$\sqrt{3}$π | D. | $\frac{27\sqrt{3}π}{2}$ |
11.定义域在R上的奇函数f(x),当x≥0时,f(x)=$\left\{\begin{array}{l}{log_{\frac{1}{2}}}({x+1}),0≤x<1\\ 1-|{x-3}|,x≥1\end{array}$,则关于x的方程f(x)-a=0(0<a<1)所有根之和为1-$\sqrt{2}$,则实数a的值为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{1}{4}$ |